リンク関数
Minitabでは、logit(デフォルト)、normit、gompitの3種類のリンク関数が利用できます。リンク関数により、広範な順位応答モデルへの適合を行うことができます。logitは標準累積ロジスティック分布関数の逆数です。normit関数は、probitとしても知られており、標準累積正規分布関数の逆数です。gompit関数は、相補的log-logとしても知られており、ゴンペルツ分布関数の逆数です。
計算式
g(χk) = θk +x'β, k = 1, ..., K-1
リンク関数は分布関数の逆関数です。リンク関数とそれらに対応する分布は以下のようにまとめられます。
| 名前 | リンク関数 | 分布 |
|---|---|---|
| logit | g(χ) = loge(χ/ (1 – χ)) | ロジスティック |
| normit(probit) |
g(χ) = Φ–1(χ) |
正規 |
| gompit(相補的log-log) | g(χ) =loge (–loge(1 – χ)) | ゴンペルツ |
表記
| 用語 | 説明 |
|---|---|
| K | 応答の異なるカテゴリ数 |
| χk | 累積確率に含まれ、最大値でもあるカテゴリk, (π1+ ...+ πk) |
| g(χk) | 予測変数のベクトル |
| θk | k番目の異なる応答カテゴリと関係のある定数 |
| x | 予測変数のベクトル |
| β | 予測変数に関連する係数のベクトル |
因子/共変量パターン
データセット内の1組の因子/共変量の値を説明します。因子/共変量パターンごとに、事象確率、残差、およびその他の診断測定値が計算されます。
たとえば、データセットに性別や人種の因子、年代の共変量が含まれている場合、これらの予測変数の組み合わせには、統計対象と同じ数のさまざまな共変量パターンが含まれている可能性があります。データセットに人種や性別の因子のみが含まれ、それぞれ2つの水準でコード化されている場合は、4つの因子/共変量パターンしかありません。データを、頻度または成功、試行、もしくは失敗として入力する場合、各行には1つの因子/共変量パターンが含まれます。
事象確率
事象確率はπk for k = 1, 2, ..., Kです。
計算式
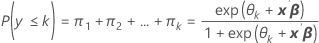
表記
| 用語 | 説明 |
|---|---|
| k | 1, ..., K – 1と等しい |
| θk | 定数 |
| β | logit式の係数のベクトル |
累積事象確率
可能なkごとに応答がkまたは以下のカテゴリに分布する確率。k番目の累積確率は以下になります。
計算式
P(y k) = p1 + ... + pk,k = 1, ... , K
k) = p1 + ... + pk,k = 1, ... , K
累積確率は応答の順位に反映されます。k応答カテゴリを持つモデルの場合は以下になります。
P(y 1) <P(y
1) <P(y 2)
2)  …
… P(y
P(y K) = 1
K) = 1

係数
Minitabでは比例オッズモデルを使用し、予測変数のベクトルxは、カテゴリkまたは以下の応答の対数オッズに対するxの影響を説明するパラメータβを持ちます。Minitabでは、すべてのK – 1カテゴリに対するxの影響は同じだと仮定するので、予測変数ごとに1つの係数しか計算されません。予測変数の係数は、kが固定の場合、参照水準と比較される1つの水準に予測変数がある場合、応答のlogitにおいて推定値が変化することを示します。
Minitabでは、K – 1カテゴリごとに定数が推定されます。パラメータ推定値を使用して、累積確率用のモデルを使用してカテゴリごとに推定確率を計算します。
計算式
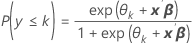
推定係数は反復再重み付け最小二乗法を使用して計算され、最尤推定値に等しくなります。1、2
参考文献
- D.W. Hosmer、S. Lemeshow(2000)、Applied Logistic Regression第2版、John Wiley & Sons, Inc.
- P. McCullagh、J.A. Nelder(1992)、Generalized Linear Model、Chapman & Hall
係数の標準誤差
漸近的な標準誤差は、推定された係数の精度を示します。標準誤差が小さいほど、推定値の精度が高くなります。
詳細は、[1]および[2]を参照してください。
- A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
- P. McCullagh、J.A. Nelder(1992)、Generalized Linear Model、Chapman & Hall
Z
Zは、予測変数が応答と有意な関係があるかどうかを判断するために使用します。Zの大きい方の絶対値は有意な関係を示します。p値は、Zが正規分布になることを示します。
計算式
Z = βi /標準偏差
定数の計算式は以下になります。
Z = θk /標準誤差
サンプルが小さい場合、尤度比検定は、より信頼できる有意性検定になり得ます。
p値(P)
p値は、仮説検定で帰無仮説を棄却できるかどうかを決定するために使用されます。p値は帰無仮説が真の場合に、実際の計算値と少なくとも同程度以上の極端な検定統計量が得られる確率です。p値用によく使用されるカットオフ値は0.05です。たとえば、検定統計量の計算されたp値が0.05未満の場合、帰無仮説を棄却します。
オッズ比
Minitabでは、順位ロジスティック回帰の比例オッズモデルを使用します。予測変数ごとに1つのパラメータと1つのオッズ比のみ計算されます。オッズ比は、累積確率とその補集合を使用します。x1とx2の2つの水準を持つ予測変数の場合、累積オッズ比は以下になります。
計算式
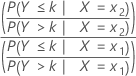
信頼区間
計算式
βi のサンプルの信頼区間が大きい場合は以下になります。
β i + Zα /2*(標準誤差)
オッズ比の信頼区間を得るには、信頼区間の上限と下限をべき乗します。信頼区間は、オッズが予測変数の単位変化ごとに分布できる範囲を示します。
表記
| 用語 | 説明 |
|---|---|
| α | 有意水準 |
対数尤度
個々の確率密度関数から派生したこの式は最大化されて、βの最適値を導き出します。対数尤度はサンプルサイズによって変わるので、適合値の指標として単独で使用することはできませんが、2つのモデルの比較には使用できます。
順位ロジスティック回帰では、kカテゴリごとに、n個の独立した多項式ベクトルがあります。これらの観測値は、y1、...、ynで表されます(yi = (yi1, ..., yik)かつΣjyij = miがiごとに固定されています)。i番目の観測値yiから、対数尤度の寄与度は以下になります。
計算式
L(πi ; yi) = Σkyik log πik
合計対数尤度は、以下のn個の観測値の各寄与度の和です。
L(π ; y) = Σi L(πi; yi)
表記
| 用語 | 説明 |
|---|---|
| πik | k番目のカテゴリに対するi番目の観測値の確率 |
分散共分散行列
次元がp + K – 1の正方行列。各係数の分散は対角セルにあり、1対の係数ごとの分散は非対角セルにあります。分散は係数を二乗した標準誤差です。
分散共分散行列は漸近的であり、情報行列を逆行列にして最後に反復したときに得られます。
表記
| 用語 | 説明 |
|---|---|
| p | 予測変数の数 |
| K | 応答のカテゴリ数 |
ピアソン
データへのモデル適合度を示すピアソン残差を基準にした要約統計量。ピアソンは、共変量の異なる値の数が観測値数とほぼ等しいときは役立ちませんが、同じ共変量水準で観測値を反復しているときは役立ちます。χ2検定統計量が高く、p値が低くなるほど、データへのモデル適合度は十分でないことを示します。
計算式は以下になります。
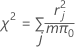
r = ピアソン残差、m = j番目の分散または共変量パターンの試行回数、π0 = 比率に対して仮定された値。
逸脱度
データへのモデル適合度を示す逸脱度残差に基づく要約統計量。逸脱度は、共変量の異なる値の数が観測値の数とほぼ等しくなる場合には役立ちませんが、同じ共変量水準で観測値を反復する場合に役立ちます。Dの値が高く、p値が低いほど、モデルがデータに十分に適合しないことを示します。検定の自由度は(k - 1)*J − (p)(kは応答のカテゴリ数、Jは因子または共変量パターン数、pは係数の数)です。
計算式は以下になります。
D =2 Σ yik log p ik− 2 Σ yik log π ik
πik = k番目のカテゴリに対するi番目の観測値の確率。
連関の測度
一致するペアと一致しないペアは、モデルがどの程度データを予測するかを示します。一致するペアが多いほど、モデルの予測能力は上がります。
一致するペアと一致しないペア、および同順位ペアの表は、異なる応答値を持つ観測値をすべての可能なペアリングをすることにより計算されます。各応答値が1、2、3であると仮定します。応答値1を持つすべての観測値は、応答値2、3を持つすべての観測値とペアになり、応答値2を持つすべての観測値は、応答値1、3を持つすべての観測値とペアになります。ペアの合計数は、応答値1を持つ観測値の数に応答値2を持つ観測値の数を掛けたものと、応答値1を持つ観測値の数に応答値3を持つ観測値の数を掛けたものと、応答値2を持つ観測値の数に応答値3を持つ観測値の数を掛けたものを足し合わせたものです。
ペアが一致するか一致しないかを決定するために、各観測値の累積予測確率が計算され、これらの値が観測値の各ペアに対して比較されます。
- 一致するペア
- 最も小さい応答値(前述の例では1)を含むペアでは、最小応答値までの累積確率が、大きな応答値を持つ確率に対してより、最小の応答値を持つ観測値に対して大きい場合、ペアは一致します。最も大きな応答値(上記の例では2と3のペア)を持つペアでは、応答値が2までの累積確率が、応答値3を持つ応答に対してより、応答値2を持つ観測値に対して大きい場合、ペアは一致します。
- 一致しないペア
- 最も小さい応答値(前述の例では1)を含むペアでは、最小応答値までの累積確率が、小さな応答値を持つ確率に対してより、大きな応答値を持つ観測値に対して大きい場合、ペアは一致しません。最も大きな応答値(上記の例では2と3のペア)を持つペアでは、応答値が2までの累積確率が、応答値2を持つ応答に対してより、応答値3を持つ観測値に対して大きい場合、ペアは一致しません。
- 同順位
- 観測値の成功と失敗の予測確率が等しい場合、ペアは同順位です。
計算式
一致するペア、一致しないペア、同順位ペアの表に基づき、Minitabでは以下の要約測度を計算します。
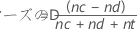


表記
| 用語 | 説明 |
|---|---|
| nc | 一致するペアの数 |
| nd | 一致しないペアの数 |
| nt | 同順位のペアの数 |
| N | 合計観測数 |
