目的の方法または計算式を選択してください。
適合値
θ*におけるn番目の観測値の期待応答:


表記
| 用語 | 説明 |
|---|---|
| θ* | 最後の反復 |
| xn | n番目の観測値における予測変数の値のベクトル |
| v0 | 勾配行列 = ( ∂f(xn, θ) / ∂θp )(Pの単位はf(x0, θ)の偏導関数の1ベクトル)はθ*で評価されます。 |
予測値の信頼区間
応答平均値が指定された予測の設定内に収まると考えられる範囲です。予測に対するおよそ100(1 - α)%の信頼区間は以下になります。
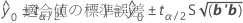
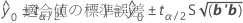
表記
| 用語 | 説明 |
|---|---|
| tα/2 | N – Pの自由度を持つt分布の上側エンドポイントαまたは2 |
| 適合値の標準誤差 | 適合値の標準誤差 |
| n | n番目の観測値 |
| N | 合計観測数 |
| P | 自由(ロックされていない)パラメータの数 |
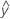 | 適合値 |
| b | (R')-1v0 |
| R | 最後の反復でViのQR分解から得られる(上三角)R行列 |
| v0 | 勾配行列 = ( ∂f(xn, θ) / ∂θp)(Pの単位はf(x0, θ)の偏導関数の1ベクトル)はθ*で評価されます。 |
| S |
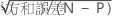 |
予測区間
1つの新しい観測値の予測応答が含まれると予想される範囲。新しい観測値が持つ、予測に対するおよそ100(1 - α)%の信頼区間は以下になります。
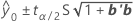
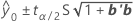
表記
| 用語 | 説明 |
|---|---|
| tα/2 | N – Pの自由度を持つt分布の上側エンドポイントαまたは2 |
| 適合値の標準誤差 | 適合値の標準誤差 |
| n | n番目の観測値 |
| N | 合計観測値数 |
| P | 自由(ロックされていない)パラメータの数 |
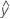 | 適合値 |
| b | (R')-1v0 |
| R | 最後の反復でViのQR分解から得られる(上三角)R行列 |
| v0 | 勾配行列 = ( ∂f(xn, θ) / ∂θp)(Pの単位はf(x0, θ)の偏導関数の1ベクトル)はθ*で評価されます。 |
| S |
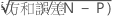 |
適合値の標準誤差
適合値の適切な標準誤差は以下になります。






表記
| 用語 | 説明 |
|---|---|
| n | n番目の観測値 |
| N | 合計観測数 |
| P | 自由(ロックされていない)パラメータの数 |
| x0 | 予測変数の値のベクトル |
 | f(x0, θ*) |
| v0 | 勾配行列 = ( ∂f(xn, θ) / ∂θp)(Pの単位はf(x0, θ)の偏導関数の1ベクトル)はθ*で評価されます |
| S |
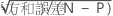 |
