目的の方法または計算式を選択してください。
パラメータ制約
パラメータを変換することによってパラメータ制約を実施します。1
| If | その後 |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| 用語 | 説明 |
|---|---|
| a、b | 数値定数 |
| θの | パラメータ |
| φ | 変換されたパラメータ |
これらの変換が実行され、元のパラメータに換算した結果が表示されます。
- Bates、Watts(1988)、Nonlinear Regression Analysis and Its Applications、John Wiley & Sons, Inc.
パラメータ推定の標準誤差
θpの推定値の近似標準誤差は、以下の対角要素pの平方根にSを掛けたものです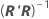 、これは以下のように記述します。
、これは以下のように記述します。

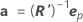

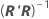 、これは以下のように記述します。
、これは以下のように記述します。

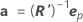

表記
| 用語 | 説明 |
|---|---|
| n | n番目の観測値 |
| N | 合計観測数 |
| p | 自由(ロックされていない)パラメータの数 |
| R | 最後の反復でViのQR分解から得られる(上三角)R行列 |
| V0 | 勾配行列 = ( ∂f(xn, θ) / ∂θp)(Pの単位はf(x0, θ)の偏導関数の1ベクトル)はθ*で評価されます |
| S |
 |
パラメータ推定の相関行列
パラメータ推定の適切な分散共分散行列は以下になります。
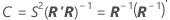
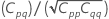

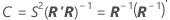
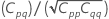

表記
| 用語 | 説明 |
|---|---|
| R | 最後の反復でViのQR分解から得られる(上三角)R行列 |
| P | 自由(ロックされていない)パラメータの数 |
| v0 | 勾配行列 = ( ∂f(xn, θ) / ∂θ p)(Pの単位はf( x0, θ)の偏導関数の1ベクトル)はθ*で評価されます。 |
| θの | パラメータ |
パラメータの尤度信頼区間を測定します。
θ = (θ1, . . . . θp) *とします(θ*はθの最後の導関数)。
尤度ベースの100 (1 - α) %信頼限界は以下を満たします。
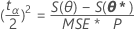
S( θp )は、θpを固定し、他のパラメータを最小化したときに得られる平方和誤差です。1これは以下の解法と等しいです。
S(θp) = S(θ*) + (tα/2)2 平方和誤差
表記
| 用語 | 説明 |
|---|---|
| θの | パラメータ |
| n | n番目の観測値 |
| N | 合計観測数 |
| P | 自由(ロックされていない)パラメータの数 |
| tα/2 | Nを持つt分布の上側点 αまたは2 - 自由度P |
| S(θ) | 平方和誤差 |
| 誤差の平均平方 | 平均平方誤差 |
- Bates、Watts(1988)、Nonlinear Regression Analysis and Its Applications、John Wiley & Sons, Inc.
