目的の方法または計算式を選択してください。
このトピックの内容
表記
観測値nの予想関数は以下によって示されます。
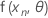
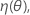
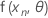 .
.

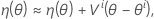
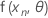
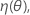
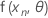 .
.
ηのヤコビアンは、以下のパラメータに関する予想関数の偏導関数と等しい要素を持つN × P行列です。

ηの線形近似は以下になります。
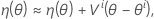
θ*が最小二乗推定値を示すとします。
ガウス・ニュートン
デフォルトでは、ガウス・ニュートン法を使用して、最小二乗推定値を判断します。この方法では、予想関数に対して線形近似を使用して、θの最初の推定θ0を繰り返し改善し、相対オフセットが指定された許容範囲1を下回るまで推定値を改善し続けます。それは、θ0の最初のテイラー級数で予想関数f(xn,θ)を以下のように拡張するということです。
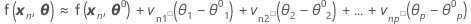
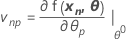
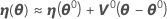

 および
および
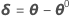


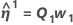
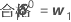 .
.

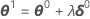
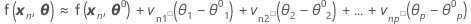
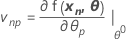
N個のケースすべてを含む
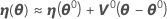

ここで、

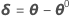
ガウスの増分δ0を計算して、近似残差平方和を最小化します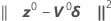 、以下を使用します。
、以下を使用します。


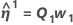
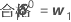 .
.
点

これはη(θ0)よりもyに近づける必要があり、値θ1 = θ0 + δ0を使用し、新しい残差z1 = y - η(θ1)、新しい導関数行列V1、および新しい増分を計算して、もう一度反復を実行します。増分が小さすぎて、パラメータのベクトルの要素に有用な変化が見られなくなるほど収束するまで、このプロセスは繰り返されます。
時には、ガウス・ニュートンの増分により、平方和が増加することがあります。これが発生すると、線形近似は、η(θ0)周辺の十分に小さな領域の実際の曲面にかなり近似します。平方和を減少させるには、ステップ因子λを導入して計算します。
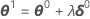
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
レーベンバーグ・マルカート
勾配行列Vの列に共線性がある場合、特異になり、ガウス・ニュートン反復の不規則な振る舞いの原因になることがあります。特異点を処理するために、ガウス・ニュートンの増分を以下のようなレーベンバーグの折衷案に変更できます。
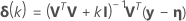
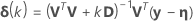
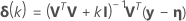
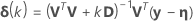
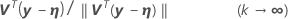 。1
。1
- Bates、Watts(1988)、Nonlinear Regression Analysis and Its Applications、John Wiley & Sons, Inc.
相対オフセット収束基準
デフォルトでは、相対オフセットが1.0e-5未満の場合、収束が宣言されます。これにより確実に、現在のパラメータのベクトルが、最小二乗の信頼領域ディスクの半径の0.001%未満であるという事実から、推論に実質的な影響を受けることがなくなります。1
1. Bates、Watts(1988)、Nonlinear Regression Analysis and Its Applications、John Wiley & Sons, Inc.
