このトピックの内容
適合線プロット
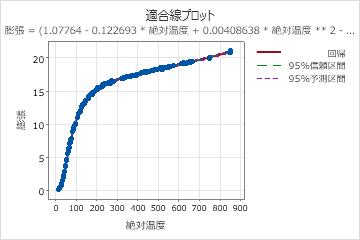
非線形モデルに1つの予測変数がある場合、Minitabは適合線プロットで予測変数と応答の関係を表示します。このプロットには、回帰式を表す回帰線が含まれます。プロット上の95%の信頼区間と予測区間を表示することを選択することもできます。
解釈
- 全予測値の範囲全体を通して、サンプルには十分な数の観測値が含まれています。
- モデルがデータの曲面性に適切に適合する。どちらのモデルが最適かを判断するには、プロット、回帰の標準誤差(S)を調べ、データに反復が含まれている場合は不適合検定での調査を行います。
- 結果に大きな影響を与える可能性のある外れ値がないか探します。外れ値がある場合は、その原因を特定してください。データ入力や測定の誤差を修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。外れ値の検出に関する詳細は、異常な観測値を参照してください。
式
回帰式を使用して、モデルにおける応答と項の関係を表します。回帰式は回帰線の代数で表現されます。各予測変数の値を式に当てはめ、平均応答値を計算します。線形回帰とは異なり、非線形回帰式はさまざまな形式を取ります。
非線形式の場合、各予測変数が応答に及ぼす影響を判断するということは、線形式の場合ほど直観的ではありません。線形モデルのパラメータ推定値とは違い、非線形モデルにおけるパラメータ推定値に対する決まった解釈はありません。各パラメータの正しい解釈は、予想関数とその中のパラメータの位置によって決まります。非線形モデルに1つしか予測変数がない場合は、適合線プロットを評価して予測変数と応答の関係を確認します。
解による収束によってモデル適合の最適性や平方和誤差(SSE)の最小化が保証されるわけではありません。平方和誤差(SSE)最小が全体ではなく一部である場合や、または予測関数が不正確なためにパラメータ値が不適切になり、その不適切なパラメータ値が原因で収束している場合もあるからです。そのため、パラメータ値、適合線プロットおよび残差プロットを調べて、モデルが適合しているか、パラメータ値が妥当であるかを判断することが極めて重要です。
解釈
この結果には、1つの予測変数と7つのパラメータ推定値があります。応答変数は膨張で、予測変数は絶対温度です。長い式で応答と予測との間の関係を記述します。絶対温度が1度上昇したときの銅の膨張に対する影響は、開始温度によって大きく異なります。温度の変更が銅の膨張に及ぼす効果は、簡単には要約できません。適合線プロットを評価し、予測変数と応答の関係を確認します。
式に温度の値を入力すると、結果は銅の膨張の適合値となります。
式
0.00576099 * 絶対温度 + 0.000240537 * 絶対温度 ** 2 - 1.23144E-07 * 絶対温度 ** 3)
95%信頼区間(CI)
適合値の信頼区間は、指定された予測を条件として、応答平均値になる可能性のある値の範囲を表します。
解釈
信頼区間を使用して、変数の観測値に関する適合値の推定値を評価します。
たとえば、信頼水準が95%の場合は、モデル内の指定された値の変数を持つ母集団が含まれる信頼区間を95%信頼できます。信頼区間は、結果の実質的な有意性を評価するのに役立ちます。専門知識を使って、信頼区間に実質的に有意な値が含まれているかどうかを状況に応じて判断します。信頼区間が広い場合、将来価値の平均値に対する信頼性が低くなります。信頼区間が広すぎて役に立たない場合、サンプルのサイズを大きくすることを検討します。
95% 予測区間(PI)
予測区間は、予測変数の設定が指定されたものとして、予測変数の値に関する将来の応答が1つ含まれる可能性のある範囲です。
解釈
たとえば、家具メーカーの材料技師は単回帰モデルを開発して、パーティクルボードの密度からそのボードの剛性を予測します。技師は、モデルが分析の仮定を満たすかどうかを検証します。その後、モデルを使用して、剛性を予測します。
回帰式は、新しい観測値の剛性が66.995になることを予測し、予測区間は[50, 85]になります。観測値の剛性値が厳密に66.995になる可能性は低いと考えられますが、予測区間は実際の値が95%の信頼度でおよそ50~85になるであろうことを示します。
単一の応答の予測は、複数の応答平均の予測よりも不確実であるため、予測区間は常に対応する信頼区間よりも広くなります。
