目的の方法または計算式を選択してください。
多項式回帰モデル
計算式
以下のような線形、2次、または3次（キューブ）回帰モデルを適合することができます。
| モデルタイプ | 次数 | 統計モデル |
|---|---|---|
| 線形 | 1番目 | Y = β0+ β1x + e |
| 2次 | 2番目 | Y = β0+ β1x + β2x2+ e |
| 3次 | 3番目 | Y = β0+ β1x + β2x2+ β3x3+ e |
曲率をモデル化する別な方法は、線形、2次、3次モデルのxおよび・またはyの対数10を使用して追加モデルを作成することです。また、Yの対数10を使用するのは、右への歪みまたは残差の一定ではない分散を減少させるためです。
Minitabが2次モデルまたは3次モデルを適合する場合、係数を推定する前に予測変数を標準化します。標準化により、予測変数の間にある多重共線性は減少します。多重共線性は非常に低くなるため、Minitabはモデルから予測変数を除外する可能性があることは、減少によって確実になります。この結果には、予測変数の元の単位で標準化係数が表示されます。
係数（Coef）
単回帰における係数または勾配の計算式は次のようになります。
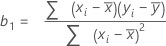
切片（b0）の計算式は以下になります。
行列の項では、重回帰の係数のベクトルを算出する計算式は以下のようになります。
b = (X'X)-1X'y
表記
| 用語 | 説明 |
|---|---|
| yi | i番目に観測された応答値 |
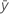 | 平均応答 |
| xi | i番目の予測変数値 |
 | 平均予測変数 |
| X | 計画行列 |
| y | 応答行列 |
S
表記
| 用語 | 説明 |
|---|---|
| 誤差の平均平方 | 誤差の平均平方 |
R二乗
その他の式は以下になります。
R2はyおよびの二乗相関としても算出することができます。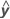
.
表記
| 用語 | 説明 |
|---|---|
| 平方和（SS） | 平方和 |
| y | 応答変数 |
 | 適合応答変数 |
自由度調整済みR二乗
表記
| 用語 | 説明 |
|---|---|
| 平均平方（MS） | 平均平方 |
| 平方和（SS） | 平方和 |
| 自由度（DF） | 自由度 |
自由度（DF）
モデルの各構成要素の自由度は次のようになります。
| 変動要因 | DF |
|---|---|
| 回帰 | p |
| エラー | n – p – 1 |
| 合計 | n – 1 |
データが特定の基準を満たし、モデルに少なくとも1つの連続予測変数または2つ以上のカテゴリ変数が含まれている場合、不適合度検定のためにある程度の自由度を使用します。基準は以下の通りです。
- データには、同じ予測値を持つ複数の観測値が含まれます。
- データには、モデルにはない追加項を推定する修正点が含まれます。
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| p | モデルの係数の個数（定数は含まれない） |
調整平方和
距離を二乗した和。平方和回帰は、モデルで説明される分散の一部です。平方和誤差はモデルでは説明されない部分で、誤差に起因します。平方和の合計は、データ内にある分散の合計です。
計算式
平方和回帰:
平方和誤差:
全体平方和:
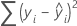
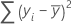
表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測反応値 |
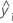 | i番目の適合された応答 |
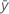 | 平均応答 |
調整平均平方…誤差
平均平方誤差（略はMS ErrorまたはMSE、表記はs2）は適合回帰線からの分散です。式は以下になります。
表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測された応答値 |
 | i番目の適合された応答 |
| n | 観測値数 |
| p | 定数を含まないモデル内の係数の数 |
調整平均平方～回帰
回帰の平均平方（MS）を表す式は以下になります。
表記
| 用語 | 説明 |
|---|---|
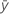 | 平均応答 |
 | i番目の適合された応答 |
| p | モデルにおける項の数 |
調整済みMS – 合計
平均平方（MS）合計の計算式は以下の通りになります。
表記
| 用語 | 説明 |
|---|---|
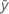 | 平均応答 |
| yi | i番目に観測された応答値 |
| n | 観測値数 |
F値
F統計量の計算式は以下の通りです。
- F（回帰）
-
- F（項）
-
- F（不適合度）
-
表記
| 用語 | 説明 |
|---|---|
| MS回帰 | 現在のモデルで説明できる応答の変動測定。 |
| MS誤差 | モデルで説明できない変動の測定。 |
| MS項 | モデル内の他の項を説明した後、項で説明できる変動量測定 |
| MS不適合度 | モデルに項を追加することで、モデル化が可能な応答の変動測定。 |
| MS純粋誤差 | 複製応答データにおける変動の測定。 |
p値～分散分析表
p値は自由度（DF）が以下であるF分布から計算される確率です。
- 分子DF
- 項の自由度の和、または検定内の項
- 分母DF
- 誤差に対する自由度
計算式
1 − P(F ≤ fj)
表記
| 用語 | 説明 |
|---|---|
| P(F ≤ f) | F分布についての累積分布関数 |
| f | 検定におけるF統計量 |
残差（Resid）
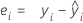
表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
 | i番目の観測された応答値 |
 | i番目の適合された応答 |
