このトピックの内容
S
Sはデータ値と適合値間の距離の標準偏差を表します。Sは応答変数の単位で測定されます。
解釈
Sを使い、モデルがどの程度良好に応答を表示するか判断します。Sは応答変数の単位で測定され、データ値と適合値の間の距離を表します。Sの値が小さければ小さいほど、モデルによる応答の記述が良好になります。ただし、Sの値が小さいだけでは、そのモデルが仮定を満たしているとは言い切れません。残差プロットを確認して仮定を検証する必要があります。
たとえば、ポテトチップ製造会社が、パッケージあたりに含まれる砕けたポテトチップの割合に影響する因子を調べるとします。モデルを有意な予測変数まで下げ、Sの計算値が1.79になったとします。この結果は、適合値を中心としたデータ点の標準偏差が1.79であることを示しています。モデルを比較している場合、1.79よりも低い値は良好な適合を示し、高い値は適合度が低いことが分かります。
R二乗
R2は、モデルによって説明される応答の変動の割合です。これは、1から合計の平方和 (モデルの全変動) に対する誤差の平方和 (モデルでは説明されない変動) の比率を引いたものとして計算されます。
解釈
R2を使用して、モデルがデータにどの程度適合するかを判断します。R2値が高いほど、データにモデルがより良く適合します。R2は常に0%から100%の間です。
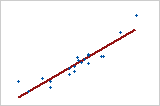
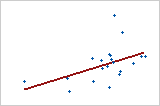
-
モデルに他の予測変数を追加すると、R2は常に増加します。たとえば、最良の5つの予測変数のモデルは、常に、低くとも、4つの予測変数のモデルと同じ高さのR2を有します。したがって、R2は、同じサイズのモデルを比較する場合にとても有用です。
-
小さなサンプルでは、応答変数と予測変数の関係の強さの正確な推定値は提供されません。たとえば、より正確にするためにR2が必要な場合は、より大きなサンプル(通常は40以上)を使用する必要があります。
-
適合度の統計量は、モデルがデータにどの程度適合するかの1つの尺度に過ぎません。モデルに望ましい値がある場合でも、残差プロットを確認して、モデルがモデルの前提を満たしていることを検証する必要があります。
自由度調整済みR二乗
調整済みR2はモデルで説明される応答の変動のパーセントで、観測値数と比較してモデル内の予測変数の数に応じて調整されます。調整されたR2は1からMSEの比を引いてMS Totalまで計算されます。
解釈
異なる数の予測変数を持つモデルを比較する場合は、調整済みR2を使用します。R2はモデルに予測変数を追加すると、それがモデルを改善しないとしても必ず大きくなります。調整済みR2値にはモデルに含まれる予測変数の数が組み入れられるため、正しいモデルの選択に役立ちます。
| モデル | ポテトの割合 | 冷却率 | 調理温度 | R2 | 調整済みR2二乗 |
|---|---|---|---|---|---|
| 0 | X | ||||
| 1 | X | X | |||
| 3 | X | X | X |
1つ目のモデルのR2は50%以上になります。2つ目のモデルでは冷却率がモデルに追加されました。調整済みR2は大きくなり、冷却率によりモデルが改善されることを示しています。調理温度が追加された3つ目のモデルでもR2は大きくなりますが、調整済みR2は大きくなりません。これらの結果から、調理温度はモデルを改善しないことがわかります。これらの結果から、調理温度はモデルを改善しないことがわかります。
