適合線プロットの例

家具製造工場の材料エンジニアは、自社が使用するパーティクルボードの剛性を評価したいと考えています。エンジニアはサンプルのパーティクルボード片の剛性と密度を測定します。

エンジニアは、単回帰を使用してパーティクルの密度とボードの剛性の間に関連性があるかどうかを調べます。

パーティクルボード.MTWサンプルデータを開きます。
統計 > 回帰 > 折れ線グラフを選択します。
応答に剛性を入力します。
予測変数に密度を入力します。
回帰モデルのタイプで、2次を選択します。
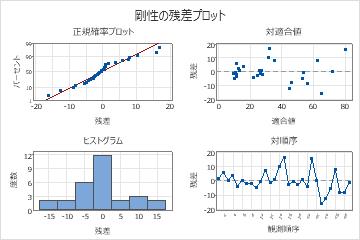
グラフをクリックします。残差プロットで、一覧表示を選択します。OKをクリックします。
オプションをクリックします。表示オプションで、信頼区間を表示すると予測区間を表示するを選択します。
各ダイアログでOKをクリックします。

結果を解釈する

分散分析表では、回帰モデルのp値は0.000であり、実際のp値は0.0005であることを意味します。p値が有意水準0.05未満なので、技師は、剛性と密度の関連性が統計的に有意であると結論付けることができます。逐次分散分析表では、線形項のp値は密度が0.000であり、2次項の場合、密度²は0.003です。どちらの値も、有意水準α=0.05より小さいです。

しかし、適合線プロットの右上隅に外れ値があるように見えます。外れ値は結果に強い影響を与えることがあるので、技師は、このデータ点を調べて、原因を判断する必要があります。

要因	自由度	平方和	平均平方	F値	p値
回帰	2	12189.4	6094.70	106.54	0.000
誤差	26	1487.3	57.21
合計	28	13676.7

要因	自由度	平方和	F値	p値
線形	1	11552.8	146.86	0.000
2次	1	636.6	11.13	0.003

適合線プロットの例

結果を解釈する

モデル要約

分散分析

逐次分散分析