重み付き回帰
重み付き最小二乗回帰は、観測値の分散が不均一な場合に用いられる手法です。分散が一定でない場合、
- 観測値の分散が大きい場合は比較的小さい重みが与えられます
- 観測値の分散が小さい場合は比較的大きい重みが与えられます
通常の重みの選択は、応答の純誤差分散の逆数です。
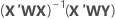
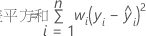
表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| X' | 計画行列の転置 |
| W | 対角線に重みを配置したn×n行列 |
| Y | 応答値のベクトル |
| n | 観測値数 |
| wi | i番目の観測値の重み値 |
| yi | i番目の観測値の応答値 |
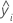 | i番目の観測値の適合値 |
ボックスーコックス変換
ボックスーコックス変換では、以下に示す通り、二乗値の残差合計を最小化するλ値が選択されます。出力される変換は、λ ≠ 0の場合にYλ、およびλ = 0の場合にln(Y)です。λ < 0の場合に、変換済み応答に−1を掛けて、変換されていない応答の順序を維持します。
−2~2の範囲で最適値が検索されます。値がこの区間外になった場合、適合性が低下することがあります。
以下は一般的な変換方法です(Y′はデータYの変換データ)。
| ラムダ(λ)値 | 変換 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 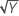 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
回帰式
複数の予測変数があるモデルの場合、回帰式は以下になります。
y = β0 + β1x1 + ... + βkxk + ε
適合する式は以下になります。
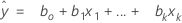
単回帰では予測変数は1つしかなく、モデルは以下になります。
y=ß0+ ß1×1+ε
回帰推定を用いて β0を β 0 、 b1 を β1 に推定すると、適合式は次のようになります。
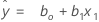
カテゴリ変数を持つ方程式
- 各カテゴリ予測レベルの別々の方程式
- 単一式
- C1
- 応答変数
- C2
- 連続予測変数
- C3
- 赤 と 青のレベルを持つカテゴリカル予測変数
- 青い:C1 = 0.184 + 0.1964*C2
- 赤い:C1 = 0.011 + 0.1964*C2
単一の方程式は、カテゴリ変数を表すために指示変数を使用します。
C1 = 0.184 + 0.1964*C2 + 0.0*C3_青- 0.173*C3_赤
- 青い観測(C3_青 = 1, C3_赤 = 0): C1 = 0.184 + 0.1964*C2 + 0.0*1- 0.173*0 = 0.184 + 0.1964*C2
- 赤い観測(C3_青 = 0, C3_赤 = 1: C1 = 0.084 + 0.1964 *C2 + 0.0*0 - 0.173*1 = 0.011 + 0.1964*C2
表記
| 用語 | 説明 |
|---|---|
| y | 応答 |
| xk | 第K期。 各項は1つの予測変数、多項式の項、または交互作用項になり得ます。 |
| ßK | k番目の 人口回帰係数 |
| ε | 平均値が0で正規分布に従う誤差項 |
| BK | 第K回 数の推定 |
 | 適合する応答 |
計画行列
計画行列では、n行(nは観測値数)の行列(X)に予測変数があります。モデル内の係数ごとに列が1つあります。
カテゴリ予測変数は、1、0、または-1、0、1のいずれかを使用してコード化されます。Xには、参照因子水準レベルの列はありません。
交互作用項の列を計算するには、交互作用の予測変数のすべての対応値を積算します。たとえば最初の観測値は予測変数Aの値が4、予測変数Bの値が2とします。計画行列では、AB間の交互作用は8(4 × 2)となります。
X'X逆行列
で回帰式から高い相関を持つ予測変数を取り除く方法 回帰モデルの適合
rijが、XiとXjに関連付けられ、現在は取り除かれた行列の要素だとします。
変数は一度に一つずつ入力されるか、削除されます。Xkは、現時点ではrkk ≥ 1(デフォルトの公差は0.0001)を持つモデルにはない独立変数である場合は入力候補となり、現在モデルにあるXjの各変数の候補にもなります。
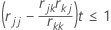
- Minitabでは、X1 … Xpをあたかもランダム変数であるかのように処理する相関行列Rに対して、SWEEP法を実行します。
- 連続予測変数の場合、rkk ≥ 公差(k = 1~p)として、要素rkkを公差と比較します。
- Xjの各変数がモデル内に現在ある場合は(rjj – rjk * (rkj / rkk)) * 公差 ≤ 1であるかどうかチェックされます。
注
ここでは、rkk、rjk、rjjは、kステップにおけるSWEEP操作の後に、XjとXkに対応する対角要素と非対角要素です。
- そうでない場合、予測値は検定に不合格となり、モデルから削除されます。
注
デフォルトの公差の値は8.8e–12です。
注
REGRESSセッションコマンドでTOLERANCEサブコマンドを使用すると、別の予測変数と相関が高い予測変数をモデル内に保持するように強制できます。ただし、公差を下げると、数値結果が不正確となる可能性があるため危険です。
