てこ比(Hi)
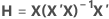
i番目の観測値のてこ比は、i番目の対角要素Hのhiです。hiの値が大きい場合、i番目の観測値は異常な予測変数(X1i, X2i, ..., Xpi)を持ちます。つまり、予測変数の値は平均ベクトル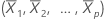 から離れているので、マハラノビス距離を使用します。
から離れているので、マハラノビス距離を使用します。
てこ比は0から1の間の値で、Minitabの異常な観測値の表では、観測値のてこ比が3p/nまたは0.99のいずれか小さい方を超えていることがXという文字によって示されます。通常は値が大きいてこ比値を調べます。
表記
| 用語 | 説明 |
|---|---|
| X | 計画行列 |
| hi | ハット行列のi番目の対角要素 |
| p | 定数項を含むモデル内の項の数 |
| n | 観測値数 |
検証のてこ比 (Hi)
計算式

重み付き回帰では、計算式に重みが含まれます。
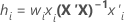
表記
| 用語 | 説明 |
|---|---|
| X | design matrix for the rows in the training data set or the folds that act as the training data set |
| xi | the vector of predictors in the i番目の validation row |
| wi | weight for the i番目の validation row |
クック(Cook)の距離
推定される回帰係数全体の観測値に対する複合的影響を測る総合的な測度、Dです。Dは、てこ比値と標準化残差を使用して計算され、観測値がx値とy値の両方について異常であるかどうかが考慮されます。D値が大きい観測値は外れ値である可能性があります。
計算式
クックの距離は、i番目の観測値を使用して計算した係数と観測値を使用せずに計算した係数との間の距離です。Minitabでは観測値を省略するたびに新たな回帰式を当てはめることなくクックの距離を計算します。計算式は以下の通りです。

表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| hi | i番目の対角要素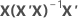 |
| p | 定数を含むモデルパラメータの数 |
| s 2 | 誤差の平均平方 |
| b | 係数ベクトル |
| b(i) | i番目の観測値を削除した後に計算した係数ベクトル |
| X | 計画行列 |
DFITS
てこ比とスチューデント化残差(削除した残差t)を結合させて1つの測度とし、観測値の異常度を測定します。DFITSは回帰モデルまたは分散分析(ANOVA)モデルの適合値に対する各観測値の影響を測定します。DFITS値が大きい観測値は外れ値である可能性があります。
DFITSは、各観測値をデータセットから取り除きモデルを再度適合させたときに適合値が変化するおおよその標準偏差を表します。Minitabでは観測値が外されるたびに、新たな回帰式を当てはめずにDFITSを計算することができます。
計算式

表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| hi | i番目の対角要素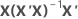 |
| X | 計画行列 |
 | i番目の適合された応答 |
 | i番目の観測値を使わずに計算された適合値 |
| 平均平方誤差 (i) | i番目の観測値を使わずに計算された誤差の平均平方 |
| n | 観測値数 |
| p | モデルのパラメータ数 |
分散拡大係数(VIF: Variance Inflation Factor)
VIFはそれぞれの予測変数を残りの予測変数について回帰分析し、R2値を割り出すことにより算出することができます。
計算式
予測変数xjの場合、VIFは以下のようになります。

表記
| 用語 | 説明 |
|---|---|
| R2( xj) | xjを応答変数、モデル内の他の項を予測変数とする決定係数 |
ダービン-ワトソンの統計量
2つの隣接する誤差項の相関が0かどうかが判断され、残差の自己相関の存在が検定されます。この検定では、誤差は最初の自己回帰の工程で作成されたという仮定に基づいています。Minitabでは、観測値は時間順などの意味のある順序に従っていることを想定しています。


表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| ei -1 | 前の観測値の残差 |
| n | 観測値数 |
