目的の方法または計算式を選択してください。
このトピックの内容
係数（Coef）
単回帰における係数または勾配の計算式は次のようになります。
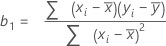
切片（b0）の計算式は以下になります。
行列の項では、重回帰の係数のベクトルを算出する計算式は以下のようになります。
b = (X'X)-1X'y
表記
| 用語 | 説明 |
|---|---|
| yi | i番目に観測された応答値 |
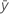 | 平均応答 |
| xi | i番目の予測変数値 |
 | 平均予測変数 |
| X | 計画行列 |
| y | 応答行列 |
係数の標準誤差（SE Coef）
単回帰では係数の標準誤差は以下になります。
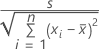
重回帰の係数の標準誤差はこの行列の対角要素の平方根です。
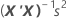
表記
| 用語 | 説明 |
|---|---|
| xi | i番目の予測変数の値 |
 | 予測変数の平均 |
| X | 計画行列 |
| X' | 計画行列の転置 |
| s2 | 誤差の平均平方 |
t値
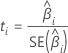
表記
| 用語 | 説明 |
|---|---|
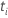 | 係数の検定統計量（ 係数） |
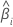 |  推定係数 |
 | 推定係数の標準誤差（ 推定係数） |
p値 - 係数表
回帰係数を0とする帰無仮説の両側p値は以下です。
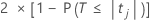
自由度は、以下に示す誤差に対する自由度です。
n – p – 1
表記
| 用語 | 説明 |
|---|---|
 | 自由度を持つt分布の累積分布関数は、誤差に対する自由度に等しくなります。 |
| tj | j番目の係数のt統計量。 |
| n | データセットに含まれる観測値の数。 |
| p | 項の自由度の和。項に定数は含まれない。 |
