目的の方法または計算式を選択してください。
平方和(SS)
行列項において、異なる平方和の計算式は以下になります。



Minitabでは、逐次平方和と調整平方和の両方を使って回帰平方和の成分または処理平方和の成分を各項で説明される変動量に分解します。
表記
| 用語 | 説明 |
|---|---|
| b | 係数のベクトル |
| X | 計画行列 |
| Y | 応答値のベクトル |
| n | 観測値数 |
| J | 全て1のn×n行列 |
遂次平方和
Minitabでは、分散のSS回帰成分または処理成分を各因子の遂次平方和に分解します。遂次平方和は、因子や予測変数をモデルに入力するときの順序によって異なります。逐次平方和は、以前に入力された因子が何かある場合、1つの因子によって説明される回帰平方和の独特の部分です。
たとえば、X1、X2、X3という3つの因子または予測変数を含むモデルがある場合、X2の遂次平方和は、X1がモデル内にすでに含まれている場合、X2によって説明される残りの変動の割合を示します。別の平方和を得るには、分析を繰り返して異なる順序で因子を入力します。
自由度(DF)
モデルの各構成要素の自由度は次のようになります。
| 変動要因 | DF |
|---|---|
| 回帰 | p |
| エラー | n – p – 1 |
| 合計 | n – 1 |
データが特定の基準を満たし、モデルに少なくとも1つの連続予測変数または2つ以上のカテゴリ変数が含まれている場合、不適合度検定のためにある程度の自由度を使用します。基準は以下の通りです。
- データには、同じ予測値を持つ複数の観測値が含まれます。
- データには、モデルにはない追加項を推定する修正点が含まれます。
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| p | モデルの係数の個数(定数は含まれない) |
調整平均平方~回帰
回帰の平均平方(MS)を表す式は以下になります。

表記
| 用語 | 説明 |
|---|---|
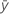 | 平均応答 |
 | i番目の適合された応答 |
| p | モデルにおける項の数 |
調整平均平方…誤差
平均平方誤差(略はMS ErrorまたはMSE、表記はs2)は適合回帰線からの分散です。式は以下になります。

表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測された応答値 |
 | i番目の適合された応答 |
| n | 観測値数 |
| p | 定数を含まないモデル内の係数の数 |
調整済みMS – 合計
平均平方(MS)合計の計算式は以下の通りになります。

表記
| 用語 | 説明 |
|---|---|
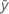 | 平均応答 |
| yi | i番目に観測された応答値 |
| n | 観測値数 |
F値
F統計量の計算式は以下の通りです。
- F(回帰)
-

- F(項)
-

- F(不適合度)
-

表記
| 用語 | 説明 |
|---|---|
| MS回帰 | 現在のモデルで説明できる応答の変動測定。 |
| MS誤差 | モデルで説明できない変動の測定。 |
| MS項 | モデル内の他の項を説明した後、項で説明できる変動量測定 |
| MS不適合度 | モデルに項を追加することで、モデル化が可能な応答の変動測定。 |
| MS純粋誤差 | 複製応答データにおける変動の測定。 |
p値~分散分析表
p値は自由度(DF)が以下であるF分布から計算される確率です。
- 分子DF
- 項の自由度の和、または検定内の項
- 分母DF
- 誤差に対する自由度
計算式
1 − P(F ≤ fj)
表記
| 用語 | 説明 |
|---|---|
| P(F ≤ f) | F分布についての累積分布関数 |
| f | 検定におけるF統計量 |
純粋誤差不適合検定
純粋誤差不適合検定の算定で、Minitabは以下の計算を行います。
- 各反復セットにおける平均からの応答の偏差の平方和を合計し純粋誤差の平方和を生成
- 純誤差の平均平方
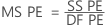

上の式で、nは観測値の数、mはx水準の組み合わせの数です。
- 不適合平方和
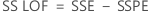
- 不適合平均平方

- 検定統計量

F値が大きい場合やp値が小さい場合は、そのモデルが不適切であると示唆しています。
p値~不適合検定
p値は、モデルに含まれていないこれらのデータから推定することができる項で全ての係数が0であるという帰無仮説検定に使います。p値は次のような自由度(DF)のF分布から算出する確率です。
- 分子DF
- 不適合に対する自由度
- 分母DF
- 純粋誤差に対する自由度
計算式
1 − P(F ≤ fj)
表記
| 用語 | 説明 |
|---|---|
| P(F ≤ fj) | F分布についての累積分布関数 |
| fj | 検定におけるF統計量 |
