ある化学研究者が、いくつかの予測変数が綿布のしわになりにくさにどのように関係するかを理解したいと考えています。化学者は、異なる処理時間、処理温度、ホルムアルデヒド濃度、触媒比の設定で製造された32個の綿セルロースを調査します。各綿布について、しわになりにくさの指標である防皺度を記録します。
化学者は、複数回の回帰分析を実行して予測変数を使用したモデルを適合し、応答に対して統計的に有意な関係を持たない予測変数を除外します。
- 標本データを開く、防皺性.MWX.
- を選択します。
- 応答に評点を入力します。
- 連続予測変数に、濃度触媒比硬化温度硬化時間を入力します。
- グラフをクリックします。
- 効果プロットのパレート図を選択します。
- 残差プロットの一覧表示を選択します。
- 残差対変数に、濃度触媒比硬化温度硬化時間を入力します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
予測変数温度、触媒比、ホルムアルデヒド濃度には、0.05の有意水準よりも小さいp値があります。これらの結果により、これらの予測変数は防しわ性に対して統計的に有意な効果を持つことが示されます。時間のp値は0.05より大きく、時間が応答に関連していると結論付けるに十分な証拠はないことがわかります。化学者は、この予測変数なしでモデルを再適合させたいと思うかもしれません。
パレート図で、温度、触媒比、ホルムアルデヒド濃度の効果は有意水準0.05において統計的に有意であることが示されています。触媒比が最も長く伸びているため、最大の効果は触媒比となります。時間の効果の伸びは最も短いため、時間の効果は最小です。
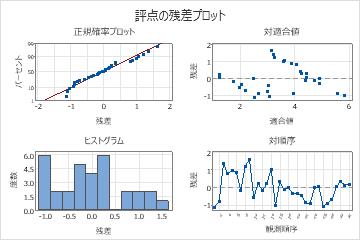
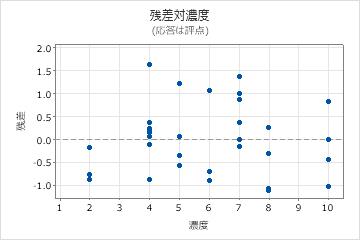
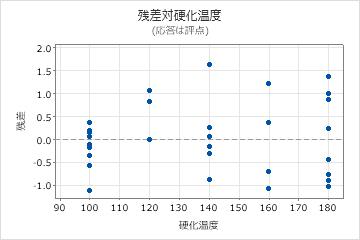
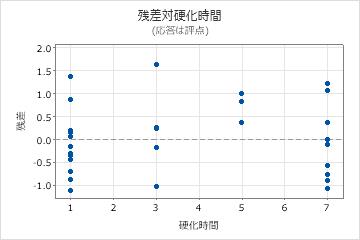
残差プロットで、モデルに問題がある可能性が示されています。
- 残差対適合値プロット上の点は、ゼロの周囲にランダムに分布していないようです。データ内の異なるグループを表す点群分布が見られるようです。化学者はそのグループを調査し、原因を特定する必要があります。
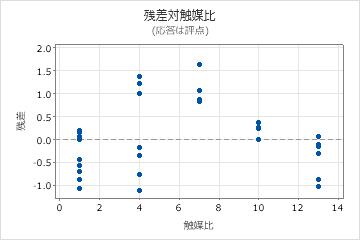
- 残差プロット対比は曲率を示し、触媒比としわに曲線関係があることがわかります。化学者は、モデルに比の2次項の追加を検討する必要があります。
回帰式
| 評点 | = | -0.756 + 0.1545 濃度 + 0.2171 触媒比 + 0.01081 硬化温度 + 0.0946 硬化時間 |
|---|
係数
| 項 | 係数 | 係数の標準誤差 | t値 | p値 | VIF |
|---|---|---|---|---|---|
| 定数 | -0.756 | 0.736 | -1.03 | 0.314 | |
| 濃度 | 0.1545 | 0.0633 | 2.44 | 0.022 | 1.03 |
| 触媒比 | 0.2171 | 0.0316 | 6.86 | 0.000 | 1.02 |
| 硬化温度 | 0.01081 | 0.00462 | 2.34 | 0.027 | 1.04 |
| 硬化時間 | 0.0946 | 0.0546 | 1.73 | 0.094 | 1.00 |
モデル要約
| S | R二乗 | R二乗 (調整済み) | R二乗 (予測) |
|---|---|---|---|
| 0.811840 | 72.92% | 68.90% | 62.81% |
分散分析
| 要因 | 自由度 | 調整平方和 | 調整平均平方 | F値 | p値 |
|---|---|---|---|---|---|
| 回帰 | 4 | 47.9096 | 11.9774 | 18.17 | 0.000 |
| 濃度 | 1 | 3.9232 | 3.9232 | 5.95 | 0.022 |
| 触媒比 | 1 | 31.0216 | 31.0216 | 47.07 | 0.000 |
| 硬化温度 | 1 | 3.6031 | 3.6031 | 5.47 | 0.027 |
| 硬化時間 | 1 | 1.9839 | 1.9839 | 3.01 | 0.094 |
| 誤差 | 27 | 17.7953 | 0.6591 | ||
| 不適合 | 25 | 17.7836 | 0.7113 | 121.94 | 0.008 |
| 純誤差 | 2 | 0.0117 | 0.0058 | ||
| 合計 | 31 | 65.7049 |
異常な観測値の適合値と診断
| 観測値 | 評点 | 適合値 | 残差 | 標準化残差 | |
|---|---|---|---|---|---|
| 9 | 4.800 | 3.178 | 1.622 | 2.06 | R |