係数
[1] P. McCullagh、J. A. Nelder(1989)Generalized Linear Models第2版、Chapman & Hall/CRC、ロンドン
係数の標準誤差
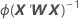
Wは対角行列であり、以下の計算式によって対角要素が求められます。
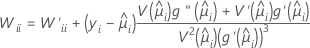
ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。Minitabで観測されたヘッセ行列を使用するのは、このモデルが、いかなる条件付平均値の誤設定に対してもロバスト性が高いためです。
正準リンクを使用した場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
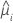 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 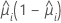 |
| ポアソン | 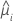 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder (1992)、Generalized Linear Model、Chapman & Hall
Z
予測変数が応答と有意な関係があるかどうかを判断するZ統計量。Zの大きい方の絶対値は有意な関係を示します。計算式は以下になります。
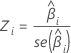
表記
| 用語 | 説明 |
|---|---|
| Zi | 標準正規分布の検定統計量 |
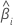 | 推定係数 |
 | 推定された係数の標準誤差 |
サンプルが小さい場合、尤度比検定は、より信頼できる有意性検定になり得ます。尤度比p値は逸脱度表に記載されています。サンプルのサイズが十分に大きい場合、Z統計量のp値は尤度比統計量のp値に近似します。
p値(P)
p値は、仮説検定で帰無仮説を棄却できるかどうかを決定するために使用されます。p値は帰無仮説が真の場合に、実際の計算値と少なくとも同程度以上の極端な検定統計量が得られる確率です。p値用によく使用されるカットオフ値は0.05です。たとえば、検定統計量の計算されたp値が0.05未満の場合、帰無仮説を棄却します。
信頼区間
推定された係数のサンプルの信頼区間が大きい場合は以下になります。
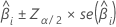
2値ロジスティック回帰について、Minitabはオッズ比の信頼区間を提供します。オッズ比の信頼区間を得るには、信頼区間の下限と上限をべき乗します。信頼区間は、オッズが予測変数の単位当たり変化量ごとに存在する範囲を示します。
表記
| 用語 | 説明 |
|---|---|
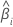 | i番目の係数 |
 | における標準正規分布の逆累積確率 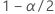 |
 | 有意水準 |
 | 推定された係数の標準誤差 |
分散共分散行列
d × dの行列では、dは予測変数の個数に1を足した数です。各係数の分散は対角セル内に、係数1対ごとの共分散は、適切な非対角セル内にあります。分散は、係数を二乗したものの標準誤差です。
分散共分散行列は、情報行列を逆行列にして最後に反復したときに得られます。分散共分散行列には次の式があります。
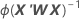
Wは対角行列であり、対角要素は以下の計算式によって求められます。

ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。結果を出すモデルは条件付き平均誤特定よりもロバスト性が高いため、Minitabでは観測されたヘッセ行列を使用します。
正準リンクが使用された場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
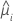 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 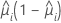 |
| ポアソン | 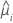 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder(1992)、Generalized Linear Model、Chapman & Hall
