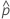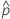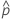2値ロジスティックモデルの当てはめと 2値ロジスティック回帰のモデル要約の方法と式

目的の方法または計算式を選択してください。

このトピックの内容

逸脱度R²
調整済み逸脱度R²
赤池情報量基準(AIC)
AICc（補正赤池情報量基準）
BIC（ベイズ情報量基準）
テストの逸脱R²
K分割逸脱R²
ROC曲線下の面積

逸脱度R²

逸脱R²は、応答の変動がモデルによって説明される量を示します。通常、R²が大きいほど、データへのモデルの適合度は高くなります。計算式は以下になります。

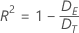
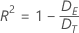
表記

用語	説明
D_E	Error Deviance
D_T値	Total Deviance

調整済み逸脱度R²

調整済み逸脱度R²は、モデル内の予測変数の数で調整されたR二乗です。予測変数の数が異なるモデルの比較に有用です。計算式は以下になります。

表記

用語	説明
R²	逸脱度R²
p	回帰自由度
Φ	1（二項モデル、ポアソンモデルの場合）
D_T	合計逸脱度

調整済み逸脱度R²の計算結果が負の値になることがありますが、こうしたケースではゼロが表示されます。

赤池情報量基準(AIC)

この統計量を使用して、異なるモデルを比較します。AICが小さいほど、データへのモデルの適合度が上がります。

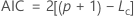
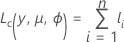
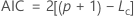
対数尤度関数は、パラメータを平均に換算して表します。関数の一般形は以下になります。

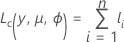
各寄与度の一般形は以下になります。

各寄与度の具体的な形式はモデルによって変わります。

モデル	l_i
二項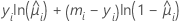
ポアソン

表記

用語	説明
p	回帰自由度
L_c	現在のモデルの対数尤度
y_i	i行目の事象数
m_i	i行目の試行数
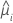	i行目の推定平均応答

AICc（補正赤池情報量基準）

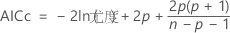
AICcは次の場合には計算されません。.

表記

用語	説明
p	モデルの係数の個数（定係数を含む）
n	欠損データを含まないデータ行の数

BIC（ベイズ情報量基準）

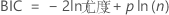
表記

用語	説明
p	定数を含まないモデル内の係数の数
n	欠損データを含まないデータ行の数

テストの逸脱R²

テストの逸脱率R²は、モデルが説明するテストデータセットの応答の変動の程度を示します。値が大きいほど、モデルはテストデータに適合します。

計算式

次式は、テストの逸脱R²の計算式を示します。

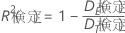
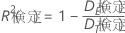
ここで、次式は誤差の逸脱を表します。

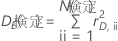
全体の逸脱度の式 D _T(テスト) は、モデルの形式によって異なります。

2値ロジスティック

切片項を持つモデルの場合、

には、次の定義があります：

切片項のないモデルの場合は、リンク関数の逆数を0にします。Minitabのリンク機能の値は、以下のとおりです：

logitリンク関数: = {0.5}
Normitリンク関数: = {0.5}
Gompitリンク関数: .

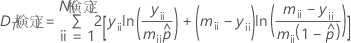
ポアソン

切片項を持つモデルの場合

切片項のないモデルの場合、

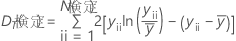
表記

用語	説明
N(検定)	データセットに含まれる行数
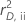	二乗逸脱残差
y_i	検定データセット内のi行目の事象数
m_i	検定データセット内のi行目の試行回数
D_E(テスト)	テストデータセットのエラー逸脱
D_T(検定)	テストデータセットの逸脱の合計

K分割逸脱R²

K分割逸脱R²は、モデルが説明する検証データセットの応答の変動の程度を示します。値が大きいほど、モデルはテストデータに適合します。

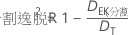
ここで、

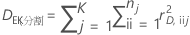
そして、D_Tは総逸脱です。

表記

用語	説明
K	分割数
n_j	分割jのサンプルサイズ
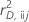	分割jのi^番目の行の交差検証済み逸脱残差

ROC曲線下の面積

計算式

曲線の下の領域は、台形の面積の合計です：

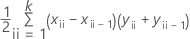
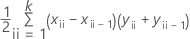
ここで、kは個別の事象確率の数であり、(x₀,y₀) は点 (0, 0) です。

テストデータセットまたは交差検証データから曲線の面積を計算するには、対応する曲線の点を使用します。

たとえば、ROC曲線上に次の座標をもつ4つの異なる事象確率があるとします。

x (偽陽性率)	y (真陽性率)
0.0923	0.3051
0.4154	0.7288
0.7538	0.9322
1	1

次に、ROC曲線下の面積は、次の計算によって与えられます。

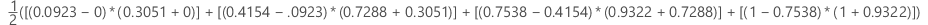
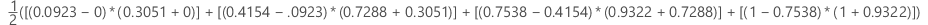
表記

用語	説明
TRP	真陽性率
FPR	偽陽性率
TP	真陽性、正しく評価された事象
P	実際の正の事象の数
FP	真陰性、正しく評価された非事象
N	実際の負の事象の数
FNR	偽陰性率
TNR	真陰性率

2値ロジスティックモデルの当てはめと 2値ロジスティック回帰の モデル要約の方法と式