係数
係数の最大尤推定値をみつける方法は2つあります。1つ目は、係数に関する尤度関数を直接最大化する方法です。これらの式は係数において非線形です。別の方法は、反復反復反復重み付け最小二乗法(IRWLS)アプローチを使用することです。McCullagh とネルダー1 は、2 つの方法が同等であることを示しています。ただし、反復再重み付け最小二乗法の方が容易に実行できます。詳細は1を参照してくてください。
k倍クロス検証の一部のケースのためのワンステップ近似法
クロス検証折り目が多い一部の大規模サンプル設計では、Minitabではクロス検証アルゴリズムで 1 ステップ近似法を使用して計算時間を短縮します (Pregibon2 および Williams3を参照)。これらの設計では、IRWLS アルゴリズムを使用したフォールドのトレーニング モデルを完全な収束に適合させるのではなく、フォールドのクロス検証統計は、アルゴリズムの最初の反復ステップからの回帰パラメータから取得されます。
次の表は、1 段階の近似値から相互検証の統計情報を取得する設計を示しています。
| サンプルサイズ(n) | 設計行列内の列数 (p) | 折り目の数 (k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p > 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p > 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p ≤ 50 | k > 1,000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p > 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p ≤ 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p > 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p ≤ 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p > 150 | k > 20 | |
| n > 100,000 | 任意の p の値 | k > 100 |
ワンステップ近似アルゴリズム
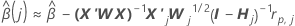
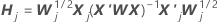
表記
| 用語 | 説明 |
|---|---|
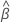 | 推定係数は完全なデータセットに適合する |
| X | 完全なデータセットの設計行列 |
| X' | 完全なデータセットの設計行列の横 |
| W | 完全なデータ セットの重み行列 |
| X'j | j番目 の折り畳みデータの設計行列 |
| Wj | j番目 の折り畳みデータの重み行列 |
| 私 | 恒等行列 |
| rp,j | j番目 のフォールドのデータの完全なデータ セットのモデルからのピアソン残差のベクトル |
[1] P. マッカラーとJ. A. ネルダー (1989).一般化された線形モデル、第2 回Ed.、チャップマン&ホール/CRC、ロンドン。
[2] D. プレギボン (1981).ロジスティック回帰診断。The Annals of Statistics, 9(4), 705-724.
[3] D. A. ウィリアムズ (1987).逸脱と単一のケースの削除を使用した一般化線形モデル診断、 適用された統計、36(2)、181-191。
係数の標準誤差
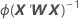
Wは対角行列であり、以下の計算式によって対角要素が求められます。
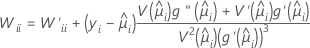
ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。Minitabで観測されたヘッセ行列を使用するのは、このモデルが、いかなる条件付平均値の誤設定に対してもロバスト性が高いためです。
正準リンクを使用した場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
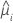 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 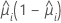 |
| ポアソン | 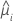 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder (1992)、Generalized Linear Model、Chapman & Hall
Z
予測変数が応答と有意な関係があるかどうかを判断するZ統計量。Zの大きい方の絶対値は有意な関係を示します。計算式は以下になります。
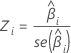
表記
| 用語 | 説明 |
|---|---|
| Zi | 標準正規分布の検定統計量 |
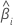 | 推定係数 |
 | 推定された係数の標準誤差 |
サンプルが小さい場合、尤度比検定は、より信頼できる有意性検定になり得ます。尤度比p値は逸脱度表に記載されています。サンプルのサイズが十分に大きい場合、Z統計量のp値は尤度比統計量のp値に近似します。
p値(P)
p値は、仮説検定で帰無仮説を棄却できるかどうかを決定するために使用されます。p値は帰無仮説が真の場合に、実際の計算値と少なくとも同程度以上の極端な検定統計量が得られる確率です。p値用によく使用されるカットオフ値は0.05です。たとえば、検定統計量の計算されたp値が0.05未満の場合、帰無仮説を棄却します。
2値ロジスティック回帰のオッズ比
2値応答をもつモデルのlogitリンク関数を選択した場合のみオッズ比が設定されます。このケースでは、オッズ比は、予測変数と応答の関係を解釈するのに役立ちます。
オッズ比(τ)はどのような非負数値にもなり得ます。オッズ比=1は、比較の基線になります。τ = 1の場合、応答と予測変数に関係はありません。τ < 1の場合、事象のオッズは、因子の参照水準に対して(または、より低い水準の連続予測変数に対して)高くなります。τ > 1の場合、事象のオッズは、因子の参照水準に対して(または、より低い水準の連続予測変数に対して)低くなります。値が1から離れるほど、関連度がより強くなることを表します。
注
2値ロジスティック回帰モデルが共変量または因子を持つ場合、成功の推定オッズは以下になります。
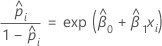
指数の関係によりβの解釈が得られます。オッズは、xが1単位増加する度にeβ1の倍数で増加します。オッズ比はexp(β1)と等しくなります。
たとえばβが0.75の場合、オッズ比はexp(0.75)であり、2.11となります。これは、xが1単位増加する度に成功のオッズが111%増加することを示しています。
表記
| 用語 | 説明 |
|---|---|
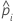 | データ内のi行目の成功の推定確率 |
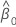 | 推定切片係数 |
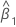 | 予測変数xの推定係数 |
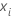 | i行目のデータ点 |
信頼区間
推定された係数のサンプルの信頼区間が大きい場合は以下になります。
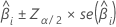
2値ロジスティック回帰について、Minitabはオッズ比の信頼区間を提供します。オッズ比の信頼区間を得るには、信頼区間の下限と上限をべき乗します。信頼区間は、オッズが予測変数の単位当たり変化量ごとに存在する範囲を示します。
表記
| 用語 | 説明 |
|---|---|
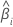 | i番目の係数 |
 | における標準正規分布の逆累積確率 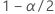 |
 | 有意水準 |
 | 推定された係数の標準誤差 |
分散共分散行列
d × dの行列では、dは予測変数の個数に1を足した数です。各係数の分散は対角セル内に、係数1対ごとの共分散は、適切な非対角セル内にあります。分散は、係数を二乗したものの標準誤差です。
分散共分散行列は、情報行列を逆行列にして最後に反復したときに得られます。分散共分散行列には次の式があります。
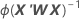
Wは対角行列であり、対角要素は以下の計算式によって求められます。

ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。結果を出すモデルは条件付き平均誤特定よりもロバスト性が高いため、Minitabでは観測されたヘッセ行列を使用します。
正準リンクが使用された場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
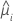 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 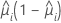 |
| ポアソン | 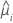 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder(1992)、Generalized Linear Model、Chapman & Hall
