残差のヒストグラム
逸脱残差のヒストグラムは、すべての観測値について残差の分布を示します。
プロットの解釈は逸脱残差またはピアソン残差のどちらを使用しても同じです。モデルにロジットリンク関数が使用されると、逸脱残差の分布は最小二乗回帰モデルの残差の分布に近くなります。予測変数設定の組み合わせに対する試行回数が増えるに連れ、逸脱残差とピアソン残差はさらに似てきます。
解釈
| パターン | パターンが示す意味 |
|---|---|
| 1つの方向に伸びている | 歪度 |
| 1本のバーが他のバーから離れている | 外れ値 |
ヒストグラムの外観は、データをグループ化するために使用されている区間の数に依存するので、残差の正規性を評価するときにヒストグラムは使用しません。その代わり、正規確率プロットを使用します。
残差の正規確率プロット
残差の正規確率プロットには、分布が正規分布する場合の残差と期待値の関係が表示されます。
プロットの解釈は逸脱残差またはピアソン残差のどちらを使用しても同じです。モデルにロジットリンク関数が使用されると、逸脱残差の分布は最小二乗回帰モデルの残差の分布に近くなります。予測変数設定の組み合わせに対する試行回数が増えるに連れ、逸脱残差とピアソン残差はさらに似てきます。
解釈
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
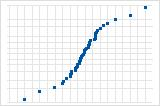
S曲線は、長い裾を持つ分布を示唆しています。
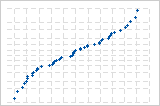
逆S曲線は、短い裾を持つ分布を示唆しています。
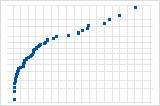
下向きの曲線は、右方向の歪みを示唆しています。
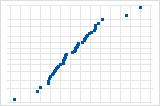
直線から離れている少数の点は、外れ値のある分布を示唆しています。
非正規パターンを閲覧する場合、他の残差プロットを使用して、項の欠落や時間順序効果などのモデルの他の問題がないかをチェックします。残差が正規分布に基づかない場合、通常の近似信頼区間とワルド検定が不正確である可能性があります。
残差対適合値
注
2値ロジスティック回帰では、データのフォーマットが2値応答/度数(1行当たりの試行回数は1回)の場合はこのプロットは作成されません。
プロットの解釈は逸脱残差またはピアソン残差のどちらを使用しても同じです。モデルにロジットリンク関数が使用されると、逸脱残差の分布は最小二乗回帰モデルの残差の分布に近くなります。予測変数設定の組み合わせに対する試行回数が増えるに連れ、逸脱残差とピアソン残差はさらに似てきます。
解釈
残差対適合値プロットを使用して、残差はランダムに分布するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不適切なリンク関数 |
| 曲線 | 高次の項の欠損または不適切なリンク関数 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |

外れ値のあるプロット
ある点が他の点に比べて大きいため、この点は外れ値となります。外れ値が多すぎる場合は、モデルが適切ではない可能性があります。外れ値の原因を識別する必要があります。データ入力や測定の誤差はすべて修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
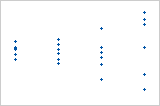
不均一分散のプロット
残差の分散が適合値の増加とともに増加しています。適合値が大きくなるにつれ、残差間でばらつきが大きくなっていることに注意してください。このパターンは、残差の分散が等しくない(不均一である)ことを示しています。
| 課題 | 可能性のある解決方法 |
|---|---|
| 不均一分散 | 別のモデル項、リンク関数または重みを使うことを検討します。 |
| 外れ値または影響力のある点 |
|
残差対データ順序
残差対データ順序プロットには、データの収集順に残差が表示されます。
プロットの解釈は逸脱残差またはピアソン残差のどちらを使用しても同じです。モデルにロジットリンク関数が使用されると、逸脱残差の分布は最小二乗回帰モデルの残差の分布に近くなります。予測変数設定の組み合わせに対する試行回数が増えるに連れ、逸脱残差とピアソン残差はさらに似てきます。
解釈
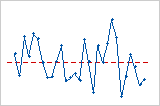
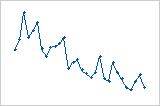
トレンド
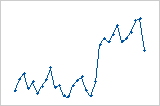
シフト
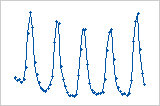
周期
残差対変数
残差対変数プロットには、別の変数に対する残差の値が表示されます。変数はモデルに取り込むことができるようになりました。あるいは、変数はモデルにないかもしれませんが、応答に影響を与えると考えられます。
プロットの解釈は逸脱残差またはピアソン残差のどちらを使用しても同じです。モデルにロジットリンク関数が使用されると、逸脱残差の分布は最小二乗回帰モデルの残差の分布に近くなります。予測変数設定の組み合わせに対する試行回数が増えるに連れ、逸脱残差とピアソン残差はさらに似てきます。
解釈
変数がすでにモデルに含まれている場合、変数のより高次の項を追加する必要があるかどうかを決定します。変数がモデルに含まれていない場合、プロットを使用して、変数が応答に体系的な影響を及ぼしているかどうかを決定します。
| パターン | パターンが示す意味 |
|---|---|
| 残差に特定のパターンがある | 変数が応答に体系的に影響を及ぼしています。変数がモデル内にない場合、その変数の項をモデルに含めて、モデルを再適合します。 |
| 点の分布に曲面性 | 変数の高次の項をモデルに取り込む必要がある。たとえば、曲線的なパターンは、2次項を追加する必要があることを示しています。 |
