逸脱度R二乗
逸脱度R2は通常、モデルが説明する応答変数の総逸脱度の比率と考えられます。
解釈
逸脱R2値が大きくなるほど、データへのモデル適合度は上がります。逸脱R2は必ず0~100%の間の値になります。
逸脱度R2は、モデルに新しい項を追加すると必ず大きくなります。たとえば、最適な5項モデルのR2は必ず、最適な4項モデルと少なくとも同じ大きさになります。したがって、逸脱度R2値は同じ大きさのモデルの比較に最も便利です。
適合度統計量は、データに対するモデルの適合度を測る1つの測度に過ぎません。モデルの値が望ましい場合でも残差プロットと適合度検定を確認してデータに対するモデルの適合度を評価する必要があります。
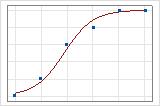
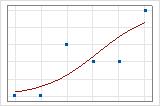
適合線プロットを使用して、異なる逸脱度R2をグラフで図示できます。1番目のプロットでは、応答の逸脱度のおよそ96%を説明するモデルが図示されます。2番目のプロットでは、応答の逸脱度の約60%を説明するモデルが図示されます。モデルが説明する逸脱度が大きいほど、データ点はより曲線に近いカーブを描きます。理論的には、モデルによって逸脱度の100%を説明できる場合、適合値は必ず観測値と等しくなり、すべてのデータ点が曲線上にプロットされることになります。
データの配列は逸脱度R2値に影響します。逸脱度R2値は通常、行ごとで単数回試行するデータよりも、行ごとで複数回試行するデータの方で高くなります。逸脱度R2値は同じデータフォーマットのモデル間でのみ比較可能です。詳細は、データフォーマットが2値ロジスティック回帰の適合値に与える影響を参照してください。
逸脱度:R二乗(調整済み)
調整済み逸脱R2はモデルで説明される応答の逸脱の比率で、観測値数と比較してモデルに含まれる予測変数に応じて調整されています。
解釈
異なる数の項を持つモデルを比較する場合は、調整済み逸脱度R2を使用します。逸脱度R2はモデルに項を追加すると必ず大きくなります。調整済み逸脱度R2値にはモデルに含まれる項の数が組み入れられるため、正しいモデルの選択に役立ちます。
| ステップ | ポテトの割合 | 冷却率 | 調理温度 | 逸脱度R2 | 調整済み逸脱度R2 | p値 |
|---|---|---|---|---|---|---|
| 0 | X | 0.000 | ||||
| 1 | X | X | 0.000 | |||
| 3 | X | X | X | 0.000 |
最初のステップでは、統計的に有意な回帰モデルが生成されます。2番目のステップでは、モデルに冷却率が追加されて、調整済み逸脱度R2が上昇します。このことから冷却率がモデルを改善することがわかります。これらの結果から、調理温度はモデルを改善しないことがわかります。これらの結果から、調理温度はモデルを改善しないことがわかります。
データの配置は逸脱度R2値に影響します。逸脱度R2は通常、行ごとに試行が1回の場合のデータより複数の試行の場合のデータの方が高くなります。調整済み逸脱度R2は、同じデータフォーマットのモデルの適合度を比較する場合にのみ使用してください。詳細は、データフォーマットが2値ロジスティック回帰の適合値に与える影響を参照してください。
テストの逸脱R二乗
解釈
テストの逸脱R2を使用して、モデルが新しいデータにどの程度適合するかを判断します。より大きなテストの逸脱R2値をもつモデルは、新しいデータでより良いパフォーマンスを発揮する傾向があります。テストの逸脱R2を使用して、さまざまなモデルのパフォーマンスを比較できます。
逸脱R2より大幅に少ないテストの逸脱R2は、モデルが過剰に適合していることを示している可能性があります。過剰に適合しているモデルは、母集団で重要でない効果に関する項を追加するときに発生します。モデルはトレーニングデータに合わせて適合されるため、母集団に関する予測を行う場合には役に立たない場合があります。
たとえば、ある金融コンサルティング会社のアナリストが、将来の市場状況を予測するモデルを開発するとします。モデルは87%のR2を有するので、有望に見えます。ただし、テストの逸脱R2は52%であり、モデルが過剰に適合している可能性があることを示しています。
高いテストの逸脱R2値自体は、モデルがモデルの前提を満たしていることを示すものではありません。残差プロットを調べて、前提を確認する必要があります。
K分割逸脱R二乗
通常、K分割逸脱R2は、モデルが説明する検証データの応答変数における全逸脱の割合と考えられます。
解釈
K分割逸脱R2を使用して、モデルが新しいデータにどの程度適合するかを判断します。より大きなK分割逸脱R2値を持つモデルは、新しいデータでより良いパフォーマンスを発揮する傾向があります。K分割逸脱R2値を使用して、さまざまなモデルのパフォーマンスを比較できます。
逸脱R2より大幅に少ないK分割逸脱R2は、モデルが過剰に適合していることを示している可能性があります。過剰適合モデルは、母集団において重要でない効果に関する項を追加するときに発生します。モデルはトレーニングデータに合わせて適合されるため、母集団に関する予測を行う場合には役に立たない場合があります。
たとえば、ある金融コンサルティング会社のアナリストが、将来の市場状況を予測するモデルを開発するとします。モデルは87%の逸脱R2を有するので、有望に見えます。ただし、K分割逸脱R2は52%であり、モデルが過剰に適合している可能性があることを示しています。
高いK分割逸脱R2値自体は、モデルがモデルの前提を満たしていることを示すものではありません。残差プロットを調べて、前提を確認する必要があります。
AIC、AICc、BIC
赤池情報量基準(AIC)、補正赤池情報量基準(AICc)、ベイズ情報量規準(BIC)は、モデルの適合度と含まれる項の数を説明する、モデルの相対的な質を測る測度です。
解釈
- AICcとAIC
- サンプルサイズがモデル内のパラメータよりも小さい場合、AICcの性能はAICよりも良くなります。サンプルサイズがかなり小さいとき、パラメーター数が多すぎるモデルではAICは小さくなる傾向があるので、AICcの性能の方が良くなります。サンプルサイズがモデルのパラメータ数に対して十分な大きさがある場合は、通常、どちらの統計量でも同じ結果が得られます。
- AICcとBIC
- AICcとBICは両方とも、モデルの尤度を評価し、モデルに項を追加したときにペナルティを適用します。このペナルティにより、モデルがサンプルデータに過剰適合する傾向を減少させます。こうした減少により、通常のモデルのパフォーマンスを改善できます。
ROC曲線下の面積
ROC曲線は、検出力とも呼ばれる真陽性率 (TPR) をy軸に、第1種の過誤とも呼ばれる偽陽性率 (FPR) をx軸にプロットします。異なるポイントは、ケースが事象である確率の異なるしきい値を表します。ROC曲線下の面積は、2値モデルが適切な分類器であるかどうかを示します。
検証法を分析に使用する場合、トレーニングデータと検証データの2つのROC曲線が計算されます。検証法が検定データセットの場合、検定のROC曲線下の面積が表示されます。検証法が交差検証の場合、K分割のROC曲線下の面積が表示されます。たとえば、10分割の交差検証の場合は、10分割のROC曲線下の面積が表示されます。
解釈
ROC曲線下の面積の範囲は、一般的に0.5から1です。2値モデルがクラスを完全に分離できる場合、曲線下の面積は1です。2値モデルがランダムな割り当てよりも良くクラスを分離できない場合、曲線下の面積は0.5です。
分析で検証法を使用する場合は、検証方法のROC曲線下の面積を使用して、モデルが新しい観測値の応答値を適切に予測できるか、または応答と予測変数の関係を適切に要約できるかどうかを判断します。トレーニングの結果は、通常、実際よりも理想的であり、参考用です。
検証法のROC曲線下の面積がROC曲線下の面積より大幅に小さい場合、その差はモデルの過剰適合を示している可能性があります。過剰適合は、母集団には重要でない項がモデルに含まれている場合に起こります。モデルはトレーニングデータに即してしまい、母集団の予測に適さなくなる可能性があります。
モデル要約
| 逸脱 (deviance) R二乗 | 逸脱 (deviance) R二乗 (調整済み) | AIC | AICc(修正済み 赤池情報量基準) | BIC(ベイズ 情報量基準) | ROC曲線下面積 | 10-分割逸脱度R二乗 | 10-分割の ROC曲線下面積 |
|---|---|---|---|---|---|---|---|
| 50.86% | 42.43% | 276.02 | 286.11 | 409.48 | 0.9282 | 17.29% | 0.8519 |
この結果では、過剰適合モデルのモデル要約表が示されています。トレーニングデータのROC曲線下の面積は、10分割のROC曲線下の面積より、モデルが新しいデータにどの程度適合するかについて、より楽観的な値を提供します。
