指数族とリンク関数
古典的線形モデルの一般化線形モデルへの拡張には2つのパートがあります。指数族の分布とリンク関数です。
指数族
1つ目のパートは、線型モデルを「指数族」と呼ばれる大きな分布族の一部である応答変数に拡張することです。指数分布族の一部には、以下のような一般形で観測された応答の確率分布関数があります。
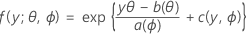
上記の式では、a(∙)、b(∙)、c(∙)は応答変数の分布によって変化します。パラメータθは、しばしば「正準パラメータ」と呼ばれる位置母数パラメータのことを指し、ϕは分散パラメータと呼ばれます。通常、関数a(ϕ)はa(ϕ)= ϕ/ ωという式が成立します。ωは既知の定数または重みであり、観測値によって変化します。(Minitabでは、重みが設定されると、関数a(ϕ)が設定に合わせて調整されます)
指数族の一部は、離散分布または連続分布になることがあります。指数族の一部となる連続分布の例として、正規分布やガンマ分布があります。指数族の一部となる離散分布の例には、二項分布とポアソン分布があります。以下の表には、このうち幾つかの分布の特徴を記載しています。
| 分布 | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| 正規 | σ2 | θ2/2 | φω |  |
| 二項 | 1 | 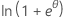 |
φ/ω | -ln(y!) |
| ポアソン | 1 | exp(θ) | φ/ω |  |
リンク関数
2つ目のパートはリンク関数です。リンク関数は、i番目の観測値の平均応答を以下の線形予測変数の式に関連付けます。
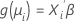
古典的線型モデルは、リンク関数が恒等関数になるような一般的な形式化の特殊ケースです。
2つ目のパートにおけるリンク関数の選択は、1つ目のパートの指数族の特定の分布によって変わります。特に、指数族の各分布には「正準リンク関数」と呼ばれる特殊なリンク関数があります。このリンク関数はg (μi) = Xi'β= θという方程式を満たし、θが正準パラメータにあたります。正準リンク関数により、このモデルの望ましい統計的性質が得られます。異なるリンク関数の適合度を比較するには、適合度の統計量を使うことができます。それまでの経緯や各分野での特殊な意味合いに応じ、使われるリンク関数は異なります。たとえば、logitリンク関数の利点の1つは、オッズ比の推定値が得られるという点です。別な例を挙げると、normitリンク関数は、2値カテゴリに分分類される正規分布に従った、基礎変数があると仮定します。
Minitabには、モデルの各クラスに対して、3つのリンク関数が用意されています。異なるリンク関数により、幅広く多様なデータに十分に適合するモデルを見つけることができます。
二項モデルの場合、リンク関数はlogit、normit(probitとも呼ばれる)、gompit(相補的log-logとも呼ばれる)です。これらは、標準累積ロジスティック分布関数の逆関数(logit)、標準累積正規分布関数の逆関数(normit)、およびゴンペルツ分布関数の逆関数(gompit)です。logitは二項モデルの正準リンク関数であるため、logitはデフォルトのリンク関数です。
ポアソンモデルの場合、リンク関数は自然対数、平方根、恒等関数です。自然対数はポアソンモデルの正準リンク関数であるため、自然対数はデフォルトのリンク関数です。
リンク関数は以下のようにまとめられます。
| モデル | 名前 | リンク関数、g(μi) |
| 二項 | logit | 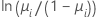 |
| 二項 | normit(probit) | 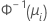 |
| 二項 | gompit(相補的log-log) |  |
| ポアソン | 自然対数 | 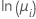 |
| ポアソン | 平方根 |  |
| ポアソン | 恒等 | 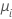 |
表記
| 用語 | 説明 |
|---|---|
| μi | i行目の平均応答 |
| g(μi) | リンク関数 |
| X | 予測変数のベクトル |
| β | 予測変数に関連する係数のベクトル |
 | 正規分布の逆累積分布関数 |
係数
[1] P. McCullagh、J. A. Nelder(1989)Generalized Linear Models第2版、Chapman & Hall/CRC、ロンドン
係数の標準誤差
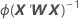
Wは対角行列であり、以下の計算式によって対角要素が求められます。
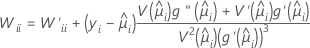
ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。Minitabで観測されたヘッセ行列を使用するのは、このモデルが、いかなる条件付平均値の誤設定に対してもロバスト性が高いためです。
正準リンクを使用した場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
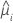 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 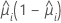 |
| ポアソン | 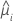 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder (1992)、Generalized Linear Model、Chapman & Hall
2値ロジスティック回帰のオッズ比
2値応答をもつモデルのlogitリンク関数を選択した場合のみオッズ比が設定されます。このケースでは、オッズ比は、予測変数と応答の関係を解釈するのに役立ちます。
オッズ比(τ)はどのような非負数値にもなり得ます。オッズ比=1は、比較の基線になります。τ = 1の場合、応答と予測変数に関係はありません。τ < 1の場合、事象のオッズは、因子の参照水準に対して(または、より低い水準の連続予測変数に対して)高くなります。τ > 1の場合、事象のオッズは、因子の参照水準に対して(または、より低い水準の連続予測変数に対して)低くなります。値が1から離れるほど、関連度がより強くなることを表します。
注
2値ロジスティック回帰モデルが共変量または因子を持つ場合、成功の推定オッズは以下になります。
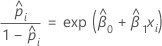
指数の関係によりβの解釈が得られます。オッズは、xが1単位増加する度にeβ1の倍数で増加します。オッズ比はexp(β1)と等しくなります。
たとえばβが0.75の場合、オッズ比はexp(0.75)であり、2.11となります。これは、xが1単位増加する度に成功のオッズが111%増加することを示しています。
表記
| 用語 | 説明 |
|---|---|
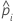 | データ内のi行目の成功の推定確率 |
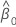 | 推定切片係数 |
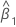 | 予測変数xの推定係数 |
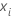 | i行目のデータ点 |
分散共分散行列
d × dの行列では、dは予測変数の個数に1を足した数です。各係数の分散は対角セル内に、係数1対ごとの共分散は、適切な非対角セル内にあります。分散は、係数を二乗したものの標準誤差です。
分散共分散行列は、情報行列を逆行列にして最後に反復したときに得られます。分散共分散行列には次の式があります。
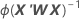
Wは対角行列であり、対角要素は以下の計算式によって求められます。

ここで

この分散共分散行列は、フィッシャーの情報行列とは対照的に、観測されたヘッセ行列に基づきます。結果を出すモデルは条件付き平均誤特定よりもロバスト性が高いため、Minitabでは観測されたヘッセ行列を使用します。
正準リンクが使用された場合、観測されたヘッセ行列とフィッシャーの情報行列は等しくなります。
表記
| 用語 | 説明 |
|---|---|
| yi | i行目の応答値 |
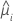 | i行目の推定平均応答 |
| V(·) | 以下の表に記載されている分散関数 |
| g(·) | リンク関数 |
| V '(·) | 分散関数の1番目の導関数 |
| g'(·) | リンク関数の1番目の導関数 |
| g''(·) | リンク関数の2番目の導関数 |
分散関数は以下のモデルによって変わります。
| モデル | 分散関数 |
| 二項 | 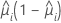 |
| ポアソン | 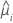 |
詳細は、[1]および[2]を参照してください。
[1] A. Agresti(1990)、Categorical Data Analysis、John Wiley & Sons, Inc.
[2] P. McCullagh、J.A. Nelder(1992)、Generalized Linear Model、Chapman & Hall
