このトピックの内容
ステップ1:モデルにおける応答と予測変数の間の関係が統計的に有意かどうか判断する
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と予測変数の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と予測変数の間に統計的に有意な関連性があると結論付けることはできません。
分散分析
| 要因 | 自由度 | 調整偏差 | 調整平均 | カイ二乗 | p値 |
|---|---|---|---|---|---|
| 回帰 | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 投薬量(mg) | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 誤差 | 4 | 0.9373 | 0.2343 | ||
| 合計 | 5 | 23.6425 |
主要な結果:p値
これらの結果では、投薬量のp値は0.000であり、有意水準の0.05未満です。これらの結果は、治療の最後における薬の投与量とバクテリアの有無の関係が統計的に有意であることを示しています。
ステップ2: 予測変数の効果を理解する
オッズ比を使用して、予測変数の影響を理解します。モデルにlogitリンク関数を使用する場合、Minitabはオッズ比を計算します。
オッズ比が1より大きい場合、予測変数が増加するにつれて事象が発生する可能性が高くなることを示しています。オッズ比が1未満の場合、予測変数が増加するにつれて事象が発生する可能性が低くなることを示しています。
連続予測変数のオッズ比
| 変更ユニット | オッズ比 | 95%信頼区間 | |
|---|---|---|---|
| 投薬量(mg) | 0.5 | 6.1279 | (1.7218, 21.8087) |
主要な結果:オッズ比
これらの結果では、モデルは薬の投与水準を使用して、成人の体内のバクテリアの有無を予測します。各錠剤に0.5mgの投与量があるので、研究者は0.5mgの単位変化を使用します。オッズ比はおよそ6です。成人が服用する錠剤が追加されるたびに、患者がバクテリアを持たないオッズ比は約6倍に増加します。
適合線プロットを使用して、応答変数と予測変数の関係を調べることができます。
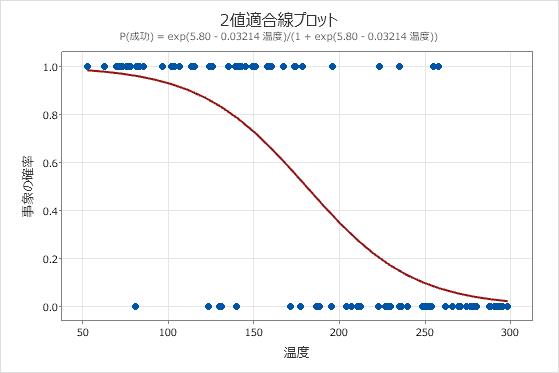
主要な結果: 2値適合線プロット
これらの結果では、式は成功確率を表しています。y軸の応答値1は成功を表します。プロットは、温度が上がると成功確率が下がることを示しています。データの温度が50に近いところでは線の傾斜はあまり大きくなく、成功確率は温度の上昇に伴い少しずつ下がることが分かります。中心部の線の傾斜はかなり大きく、この範囲では温度が1度変わるごとに結果が大きく影響されることが分かります。最高温度付近で成功確率が0に近づくと、線はまた水平になります。
ステップ3:データに対するモデルの適合度を判断する
どの程度モデルがデータに適合するかを判断するには、モデル要約表の統計量を調べます。2値ロジスティック回帰では、データのフォーマットは、AICではなく逸脱R2値に影響します。詳細はデータフォーマットが2値ロジスティック回帰の適合値に与える影響を参照してください。
- 逸脱度R二乗
-
逸脱R2値が大きくなるほど、データへのモデル適合度は上がります。逸脱R2は必ず0~100%の間の値になります。
逸脱R2はモデルに新しい予測変数を追加すると必ず大きくなります。たとえば、最適な5予測変数モデルのR2は必ず、最適な4予測変数モデルと少なくとも同じ大きさになります。したがって、逸脱R2値は同じ大きさのモデルの比較に最も便利です。
2値ロジスティック回帰では、データのフォーマットは逸脱R2値に影響します。逸脱R2は通常、データのフォーマットが事象・試行の場合に高くなります。逸脱R2値は同じデータフォーマットのモデル間でのみ比較可能です。
逸脱R2は、データに対するモデルの適合度を測る1つの測度にすぎません。モデルのR2が高い場合、残差プロットを確認して、データへのモデル適合度を評価する必要があります。
- 逸脱度R二乗(調整済み)
-
異なる数の予測変数を持つモデルを比較する場合は、調整済み逸脱R2を使用します。逸脱R2はモデルに予測変数を追加すると必ず大きくなります。調整済み逸脱R2値にはモデルに含まれる予測変数の数が組み入れられるため、正しいモデルの選択に役立ちます。
- AIC、AICc、BIC
- 2値適合線プロットでは、情報基準を使用して、異なるリンク関数または予測変数の適合値と比較できます。小さい値が好ましいと考えられます。ただし、最小値を持つモデルは必ずしもデータに良好に適合しません。検定と残差プロットも使用して、データに対するモデルの適合度を評価してください。
モデル要約
| 逸脱 (deviance) R二乗 | 逸脱 (deviance) R二乗 (調整済み) | AIC | AICc(修正済み 赤池情報量基準) | BIC(ベイズ 情報量基準) | ROC曲線下面積 |
|---|---|---|---|---|---|
| 96.04% | 91.81% | 10.63 | 14.63 | 10.22 | 0.9398 |
主要な結果:逸脱度R二乗、逸脱度R二乗(調整済み)、AIC
これらの結果を基に、モデルは、応答変数における変動のおよそ96.04%を説明づけます。こうしたデータの場合、逸脱度R2の値は、モデルがデータに十分に適合することを示しています。新しいモデルが別の予測変数と適合する場合は、他の値を使ってモデルの適合度を比較してください。
ステップ4: モデルが分析の過程を満たすかどうか判断する
残差プロットを使用して、モデルが適切か、分析の仮定が満たされているかどうかを判断しやすくします。仮定を満たさない場合、そのモデルはデータにあまり適合しない可能性があり、結果の解釈は慎重に行う必要があります。
残差プロットのパターンを処理する方法の詳細は2値適合線プロットのグラフを参照し、ページ上部にある一覧の中から残差プロット名をクリックしてください。
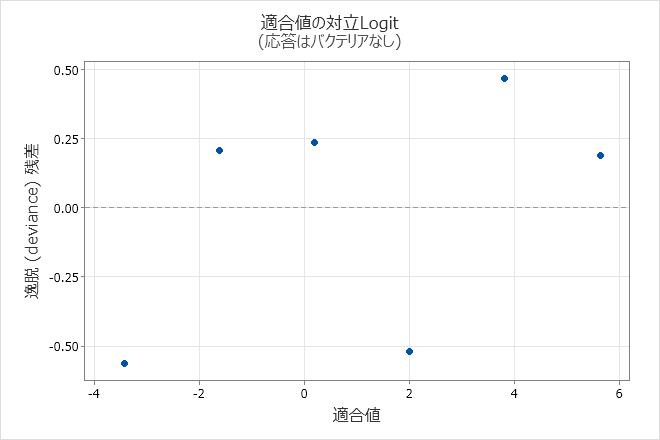
残差対適合値プロット
残差対適合値プロットを使用して、残差はランダムに分布するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
残差対適合プロットは、データが事象・試行フォーマットの場合のみ利用できます。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不適切なリンク関数 |
| 曲線 | 高次の項の欠損または不適切なリンク関数 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |
残差対順序プロット
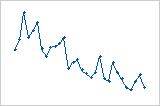
トレンド
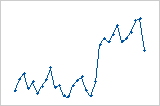
シフト
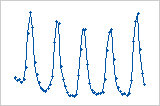
周期