ある医療研究者が、新しい薬の投与量水準が大人の体内のバクテリアの存在に及ぼす影響について知りたいと考えています。研究者は30人の患者に対して6つの投与量水準を使用して実験を行いました。研究者は、2週間にわたって、各投与量水準の薬を5人ずつの患者に与えます。2週間後、各患者はバクテリアが検出されるかどうかの検査を受けます。
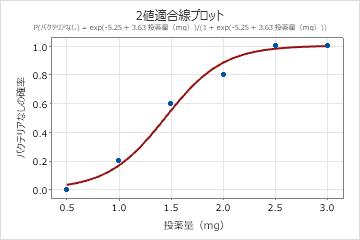
データには2値応答と1つの連続予測変数が含まれる、研究者は、2値適合線プロットを使用して薬の投与量がバクテリアの存在に関係しているかどうかを調べます。
- 標本データを開く、 バクテリア薬.MWX.
- を選択します。
- ドロップダウンリストから、事象/試行フォーマットでの応答を選択します。
- 事象名に、バクテリアなしと入力します。
- 事象数に「バクテリアなし」を入力します。
- 試行回数に試行回数を入力します。
- 予測変数に「投薬量(mg)」を入力します。
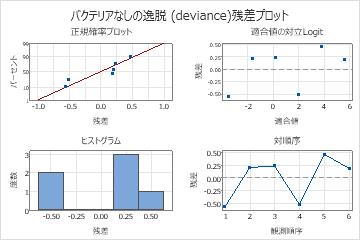
- グラフをクリックします。残差プロットで、一覧表示を選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
投薬量のp値は有意水準の0.005未満です。これらの結果は、薬の投与量とバクテリアの有無の関係が統計的に有意であることを示しています。2値適合線プロットは、投薬量が増加するにつれて、バクテリアが存在しないという対数尤度が増加します。さらに、オッズ比は、投薬水準が1mgずつ増加するのに対して、バクテリアが存在しないという対数尤度はおよそ38倍増加します。適合線プロットは、モデルがデータに適合することを示し、残差プロットはモデルに問題がないことを示します。
方法
| リンク関数 | Logit |
|---|---|
| 使用中の行 | 6 |
応答情報
| 変数 | 値 | 計数 | 事象名 |
|---|---|---|---|
| バクテリアなし | 事象 | 18 | バクテリアなし |
| 非事象 | 12 | ||
| 試行回数 | 合計 | 30 |
回帰式
| P(バクテリアなし) = exp(-5.25 + 3.63 投薬量(mg))/(1 + exp(-5.25 + 3.63 投薬量(mg))) |
|---|
係数
| 項 | 係数 | 係数の標準誤差 | VIF |
|---|---|---|---|
| 定数 | -5.25 | 1.99 | |
| 投薬量(mg) | 3.63 | 1.30 | 1.00 |
連続予測変数のオッズ比
| オッズ比 | 95%信頼区間 | |
|---|---|---|
| 投薬量(mg) | 37.5511 | (2.9647, 475.6190) |
モデル要約
| 逸脱 (deviance) R二乗 | 逸脱 (deviance) R二乗 (調整済み) | AIC | AICc(修正済み 赤池情報量基準) | BIC(ベイズ 情報量基準) |
|---|---|---|---|---|
| 96.04% | 91.81% | 10.63 | 14.63 | 10.22 |
分散分析
| 要因 | 自由度 | 調整偏差 | 調整平均 | カイ二乗 | p値 |
|---|---|---|---|---|---|
| 回帰 | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 投薬量(mg) | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 誤差 | 4 | 0.9373 | 0.2343 | ||
| 合計 | 5 | 23.6425 |