計算ルーチン
ベストサブセット回帰では、Minitabは、すべての有効な予測変数サブセットを、ステップごとに1サブセットずつ計算する方法であるハミルトニアン・ウォークと呼ばれるプロシージャを使用します。つまり、Minitabは、2**m - 1ステップ(mはモデル内の予測変数の数)ですべての2**m - 1サブセットを計算します。Minitabは、ステップごとに異なるサブセット回帰を評価します。
ハミルトニアン・ウォークの各サブセットは、1つの変数のみを追加または削除することにより、前のサブセットから変わります。スイープ演算子はハミルトニアン・ウォークのステップごとの回帰の内側または外側にある変数を「掃除」し、サブセットごとにR2を計算します。
回帰式
複数の予測変数があるモデルの場合、回帰式は以下になります。
y = β0 + β1x1 + … + βkxk + ε
適合する式は以下になります。
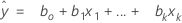
単回帰では予測変数は1つしかなく、モデルは以下になります。
y=ß0+ ß1x1+ε
ß0に対してb0、ß1に対してb1の回帰推定値を使用すると、適合する等式は以下になります。
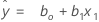
表記
| 用語 | 説明 |
|---|---|
| y | 応答変数 |
| xk | k番目の項。各項は、1つの予測変数、多項式の項、または交互作用項になり得ます。 |
| ßk | k番目の母集団回帰係数 |
| ε | 平均値が0で正規分布に従う誤差項 |
| bk | k番目の母集団回帰係数の推定値 |
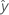 | 適合する応答 |
R二乗
R2は、決定係数とも言います。
計算式

表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測された応答値 |
 | 平均応答 |
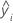 | i番目の適合された応答 |
自由度調整済みR二乗

表記
| 用語 | 説明 |
|---|---|
| 平均平方(MS) | 平均平方 |
| 平方和(SS) | 平方和 |
| 自由度(DF) | 自由度 |
予測残差平方和
モデルの予測能力を評価します。計算方法は以下の通りです。


表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| ei | i番目の残差 |
| hi | 以下のi番目の対角要素 X (X' X)-1X' |
R二乗(予測)

R2(予測)値に負値が算出される場合がありますが、Minitabでは0を表示します。
表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測された応答値 |
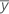 | 平均応答 |
| n | 観測値数 |
| ei | i番目の残差 |
| hi | X(X'X)–1X'のi番目の対角要素 |
| X | 計画行列 |
マローズのCp
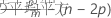
表記
| 用語 | 説明 |
|---|---|
| 誤差平方和p | 検討中モデルの平方和の誤差 |
| 平均平方誤差m | 候補となる全ての項を含むモデルの平均平方誤差 |
| n | 観測値数 |
| p | 定数項を含むモデル内の項の数 |
S

表記
| 用語 | 説明 |
|---|---|
| 誤差の平均平方 | 誤差の平均平方 |
対数尤度
非加重分析の場合、次の式を使用します。


観測値に重みが設定されている分析の場合、次の式を使用します。
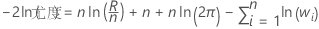
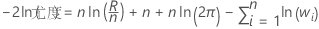
重みが0の観測値は分析に使用されません。
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| 不合格 | モデルの誤差の平方和 |
| wi | i番目の観測値の重み値 |
AICc(補正赤池情報量基準)
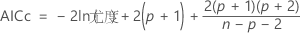
AICcは次の場合には計算されません。 .
.
表記
| 用語 | 説明 |
|---|---|
| n | 観測値数 |
| p | モデルの係数の個数(定係数を含む) |
BIC(ベイズ情報量基準)
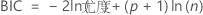
表記
| 用語 | 説明 |
|---|---|
| p | モデルの係数の個数(定係数を含む) |
| n | 観測値数 |
条件数
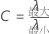
表記
| 用語 | 説明 |
|---|---|
| C | 条件数 |
| λ最大値 | モデル内の項の相関行列の固有値の最大値(切片は含まれない) |
| λ最小値 | モデル内の項の相関行列の固有値の最小値(切片は含まれない) |
