注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
研究チームは、借り手と不動産の場所に関するデータを使用して、住宅ローンの金額を予測したいと考えています。変数には、借り手の収入、人種、性別、および物件の国勢調査地区の場所、借り手と財産の種類に関するその他の情報が含まれます。
重要な予測変数を特定するための CART® 回帰 最初の調査の後、チームは必要なフォローアップステップとして考慮 TreeNet® 回帰 します。研究者たちは、応答と重要な予測変数との関係をより深く洞察し、より正確に新しい観測を予測したいと考えています。
これらのデータは、連邦住宅ローン銀行の住宅ローンに関する情報を含む公開データセットに基づいています。元データはfhfa.govです。
- 住宅ローンの購入.MTWサンプルデータを開きます。
- を選択します。
- 応答にを入力します貸付金額。
- に 連続予測変数– 地区収入を入力します 年収 。
- に カテゴリ予測変数– コアベースの統計領域を入力します 初めての家屋購入者 。
- 検証をクリックします。
- 検証法でK分割交差検証を選択します。
- 分割数 (K)に、3と入力します。
- 各ダイアログボックスのOKをクリックします。
結果を解釈する
この分析では、Minitabは300本の木を増加させ、最適な木の数は300本です。最適な木の数が、モデルが成長する木の最大数に近いため、木の数を増やして再実行します。
モデル要約
| 合計予測変数 | 34 |
|---|---|
| 重要な予測変数 | 19 |
| 増加した木の数 | 300 |
| 最適な木の数 | 300 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 94.02% | 84.97% |
| 二乗平均平方根誤差（RMSE） | 32334.5587 | 51227.9431 |
| 平均平方誤差 (MSE) | 1.04552E+09 | 2.62430E+09 |
| 平均絶対偏差 (MAD) | 22740.1020 | 35974.9695 |
| 平均絶対パーセント誤差（MAPE） | 0.1238 | 0.1969 |
500 本のツリーを含む例
- 結果で選択します ハイパーパラメータの調整 。
- 木の数に、500と入力します。
- 結果を表示をクリックします。
結果を解釈する
この分析では、500本の木が増加し、精度基準の最適値を持つハイパーパラメーターの組み合わせとして最適な木の数は500です。サブサンプル割合は、元の分析の0.5の代わりに0.7に変更されます。学習率は、元の分析の0.04372の代わりに0.0437に変更されます。
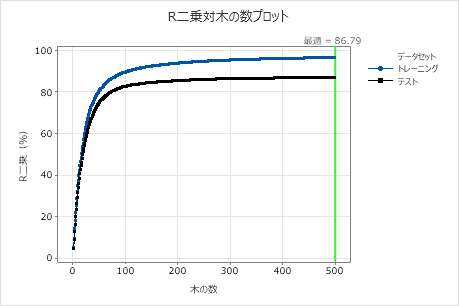
モデル要約表とR二乗対木の数プロットの両方を確認します。木の数が500のときのR2 値は、テストデータでは86.79%、学習データでは96.41%です。これらの結果は、従来の回帰分析とよりも改善されていますCART® 回帰。
方法
| 損失関数 | 二乗誤差 |
|---|---|
| 木の最適な数の選択基準 | 最大R二乗 |
| モデル検証 | 3分割交差検証 |
| 学習率 | 0.04372 |
| サブサンプルの割合 | 0.5 |
| 木あたりの最大終端ノード | 6 |
| 最小終端節サイズ | 3 |
| ノード分岐に対して選択された予測変数の数 | 予測変数の合計数 = 34 |
| 使用中の行 | 4372 |
応答情報
| 平均 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
方法
| 損失関数 | 二乗誤差 |
|---|---|
| 木の最適な数の選択基準 | 最大R二乗 |
| モデル検証 | 3分割交差検証 |
| 学習率 | 0.001, 0.0437, 0.1 |
| サブサンプルの割合 | 0.5, 0.7 |
| 木あたりの最大終端ノード | 6 |
| 最小終端節サイズ | 3 |
| ノード分岐に対して選択された予測変数の数 | 予測変数の合計数 = 34 |
| 使用中の行 | 4372 |
応答情報
| 平均 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
ハイパーパラメータの最適化
| モデル | 最適な木の数 | R二乗（%） | 平均絶対偏差 | 学習率 | サブサンプルの割合 | 最大終端ノード |
|---|---|---|---|---|---|---|
| 1 | 500 | 36.43 | 82617.1 | 0.0010 | 0.5 | 6 |
| 2 | 495 | 85.87 | 34560.5 | 0.0437 | 0.5 | 6 |
| 3 | 495 | 85.63 | 34889.3 | 0.1000 | 0.5 | 6 |
| 4 | 500 | 36.86 | 82145.0 | 0.0010 | 0.7 | 6 |
| 5* | 500 | 86.79 | 33052.6 | 0.0437 | 0.7 | 6 |
| 6 | 451 | 86.67 | 33262.3 | 0.1000 | 0.7 | 6 |
モデル要約
| 合計予測変数 | 34 |
|---|---|
| 重要な予測変数 | 24 |
| 増加した木の数 | 500 |
| 最適な木の数 | 500 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 96.41% | 86.79% |
| 二乗平均平方根誤差（RMSE） | 25035.7243 | 48029.9503 |
| 平均平方誤差 (MSE) | 6.26787E+08 | 2.30688E+09 |
| 平均絶対偏差 (MAD) | 17309.3936 | 33052.6087 |
| 平均絶対パーセント誤差（MAPE） | 0.0930 | 0.1790 |
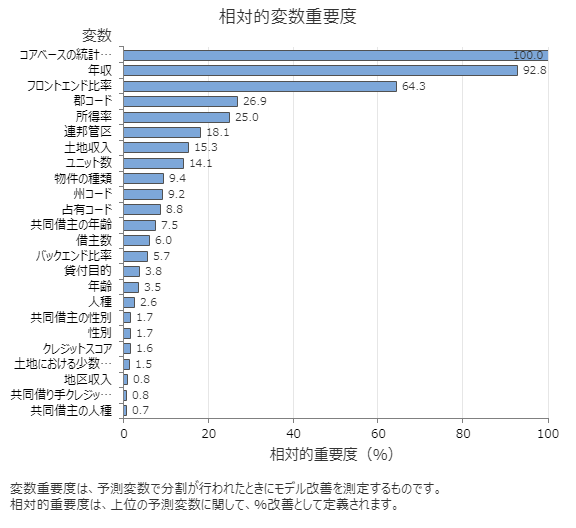
相対変数重要度グラフは、木のシーケンスに対して予測変数で分岐が行われたときに、モデルの改善に対する予測変数の効果の順に予測変数をプロットします。最も重要な予測変数は、コアベース統計領域です。上位の予測変数であるコアベースの統計領域の重要度が100%の場合、次に重要な変数である年収の寄与度は92.8%です。これは、借り手の年収が不動産の地理的位置の92.8%重要であることを意味します。
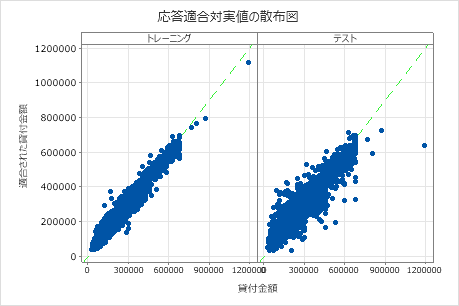
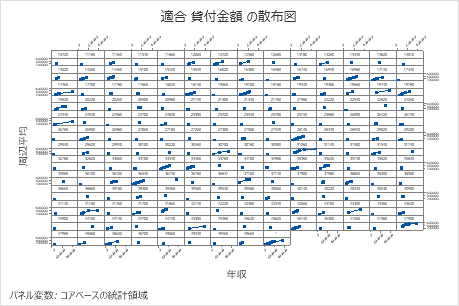
適合済みローン金額と実際のローン金額の散布図は、トレーニングデータとテストデータの両方の適合済み値と実際の値の関係を示しています。グラフ上のポイントにカーソルを合わせると、プロットされた値をより簡単に確認できます。この例では、すべての点が y=x の参照線の近くに落ちます。
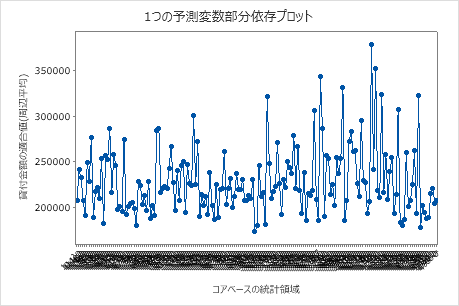
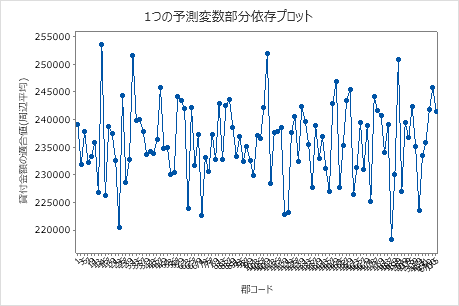
偏依存プロットを使用して、重要な変数または変数のペアが適合応答値にどのように影響するかについての洞察を得ます。部分依存プロットは、応答と変数の関係が線形、単調、またはより複雑であるかどうかを示します。
最初のプロットは、各コアベースの統計面積の適合ローン金額を示しています。データポイントが非常に多いため、個々のデータポイントにカーソルを合わせると、特定のX値とy値を確認できます。たとえば、グラフの右側の最も高いポイントはコアエリア番号41860で、適合ローンの金額は約$378069です。
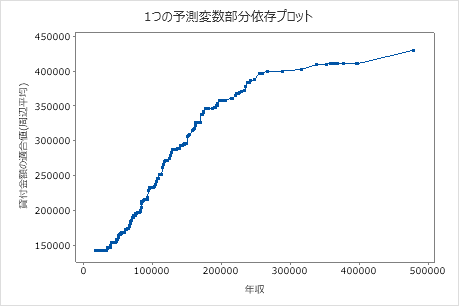
2番目のプロットは、年収が増加するにつれて適合ローン金額が増加することを示しています。年収が300000ドルに到達した後、適合ローンの金額レベルの上昇率は低下します。
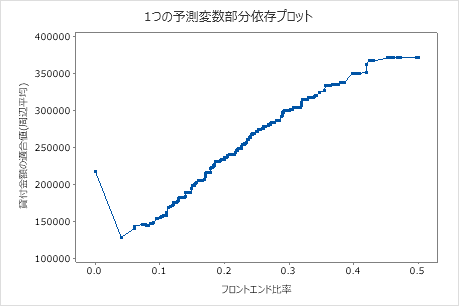
3番目のプロットは、フロントエンド比率が増加するにつれて適合ローン金額が増加することを示しています。
4 番目のプロットは、各国勢調査郡コードの調整ローン額を示しています。最初のプロットと同様に、特定のデータポイントにカーソルを合わせて、より多くの情報を得ることができます。[または ] を選択して 、他の変数のプロットを生成します。
