注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
重要な予測変数
- 予測変数がノードを分岐したときの平均二乗誤差の減少を見つけます。
- 予測変数がノード分岐であるすべてのノードからすべての減少を追加します。
次に、予測変数の重要度スコアは、すべての木でモデル改善スコアの合計と等しくなります。
2値応答の平均対数尤度
トレーニングデータまたは検証なし
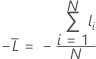
ここで、
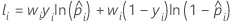
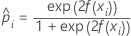
トレーニングデータまたは検証なしの場合の表記
| 用語 | 説明 |
|---|---|
| N | 完全なデータまたはトレーニングデータセットのサンプルサイズ |
| wi | 完全なデータセットまたはトレーニングデータセット内のi番目の観測の重み |
| yi | 完全またはトレーニングデータセットに対するi番目の応答値、事象の場合は1、それ以外の場合は0 |
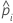 | 完全なデータセットまたはトレーニングデータセット内のi番目の行の事象の予測確率 |
 | モデルからの適合値 |
K分割交差検証
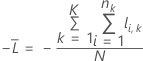
ここで、
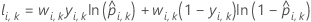
K分割交差検証の表記
| 用語 | 説明 |
|---|---|
| N | 完全なデータまたはトレーニングデータのサンプルサイズ |
| nk | 分割kのサンプルサイズ |
| wi, k | 分割kのi番目の観測値の重み |
| yi, k | 分割kにおけるケースiの2値応答値。事象クラスの場合はyi, k = 1、それ以外の場合は0。 |
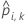 | 分割kにおけるケースiの予測確率。予測される確率は、分割kにおけるデータを使用しないモデルからのものです。 |
 | 分割kにおけるケースiの適合値。適合値は、分割kにおけるデータを使用しないモデルからのものです。 |
テストデータセット
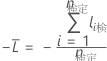
ここで、
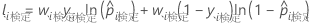
テストデータセットの表記
| 用語 | 説明 |
|---|---|
| nTest | テストデータセットのサンプルサイズ |
| wi, Test | テストデータセット内のi番目の観測値の重み |
| yi, Test | テストデータセットの分割kにおけるケースiの2値応答値。事象クラスの場合はyi, k = 1、それ以外の場合は0。 |
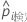 | テストセット内のケース i の予測確率 |
 | テストデータセット内のケースiの適合値 |
多項応答の平均対数尤度
は応答変数の水準数
トレーニングデータまたは検証なし
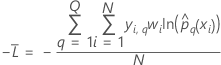
ここで、
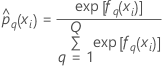
トレーニングデータまたは検証なしの場合の表記
| 用語 | 説明 |
|---|---|
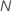 | 完全なデータまたはトレーニングデータセットのサンプルサイズ |
| wi | 完全なデータセットまたはトレーニングデータセット内のi番目の観測の重み |
| yi, q | i番目の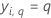
それ以外の場合は 0 |
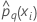 | 完全なデータセットまたはトレーニングデータセット内のi番目における応答の、 q番目の水準の予測確率 |
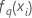 | i番目の行のq番目の木の系列からの適合値、これは応答のq番目の水準の予測確率を計算するために使用されます。 |
K分割交差検証
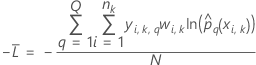
ここで、
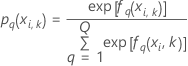
K分割交差検証の表記
| 用語 | 説明 |
|---|---|
| N | トレーニングデータのサンプルサイズ |
| nk | 分割kのサンプルサイズ |
| wi, k | 分割kのi番目の観測値の重み |
| yi, k, q | 分割kにおけるケースiのi番目の応答値、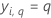
それ以外の場合は 0。 |
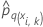 | 分割kにおけるi番目における応答の、 q番目の水準の予測確率予測される確率は、分割kにおけるデータを使用しないモデルからのものです。 |
 | 分割kにおけるi番目の行のq番目の木の系列からの適合値、これは応答のq番目の水準の予測確率を計算するために使用されます。適合値は、分割kにおけるデータを使用しないモデルからのものです。 |
テストデータセット
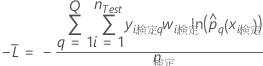
ここで、
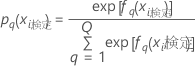
テストデータセットの表記
| 用語 | 説明 |
|---|---|
| nTest | テストデータのサンプルサイズ |
| wi, Test | テストデータ内のi番目の観測値の重み |
| yi, Test, q | テストデータセットにおけるケースiのi番目の応答値、
 それ以外の場合は
0。 |
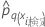 | テストデータのi番目における応答の、q番目の水準の予測確率。予測確率は、テストデータを使用しないモデルからのものです。 |
 | テストデータのi番目の行のq番目の木の系列からの適合値、これは応答のq番目の水準の予測確率を計算するために使用されます。予測確率は、テストデータを使用しないモデルからのものです。 |
ROC曲線下の面積
計算式
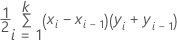
ここで、kは個別の事象確率の数であり、(x0,y0) は点 (0, 0) です。
テストデータセットまたは交差検証データから曲線の面積を計算するには、対応する曲線の点を使用します。
表記
| 用語 | 説明 |
|---|---|
| TPR | 真陽性率 |
| FPR | 偽陽性率 |
| TP | 真陽性、正しく評価された事象 |
| FN | 偽陰性、誤って評価された事象 |
| P | 実際の正の事象の数 |
| FP | 偽陽性、誤って評価された非事象 |
| N | 実際の負の事象の数 |
| FNR | 偽陰性率 |
| TNR | 真陰性率 |
例
| x (偽陽性率) | y (真陽性率) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
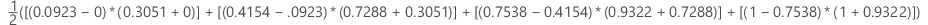
ROC曲線下の面積に対する95%信頼区間
次の区間は、信頼区間の上限と下限を示します。
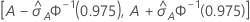
ROC曲線下の面積の標準誤差の計算(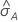
)はSalford
Predictive
Modeler®からのものです。ROC曲線下の面積の分散の推定に関する一般的な情報は、次の参考資料を参照してください。
Engelmann, B. (2011).Measures of a ratings discriminative power: Applications and limitations.In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer。doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005).Confidence intervals for the area under the ROC curve.Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., & Baumgartner, R. (2017).A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size.Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
表記
| 用語 | 説明 |
|---|---|
| A | ROC曲線下の面積 |
 | 標準正規分布の0.975百分位数 |
リフト
累積リフトの一般的な計算を表示するには、TreeNet® 分類による適合モデルおよび主要な予測変数を検出のリフトチャートの方法と計算式を参照してください。
誤分類率
重み付きの場合、カウント数の代わりに重み付きカウント数を使用します。
K分割交差検証の場合、誤分類カウント数は、各分割がテストデータセットである場合の誤分類の合計です。
テストデータセットを使用した検証の場合、誤分類カウント数はテストデータセット内の誤分類の合計であり、合計カウント数はテストデータセットの値です。
