注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
TreeNet®モデルは、単一分類または回帰木よりもさらに正確でオーバーフィットに対する耐性を備えた分類と回帰の問題を解決するためのアプローチです。プロセスの広範な一般的な説明は、最初のモデルとして小さな回帰木から始めることです。その木から、次の回帰木の応答変数となるデータのすべての行の残差が表示されます。次に、最初の木の残差を予測し、結果として得られる残差を計算するために、別の小さな回帰木を構築します。検証法を使用して、最小予測誤差を持つ最適な木の数がで特定されるまでこのシーケンスを繰り返します。木の結果のシーケンスは、TreeNet® 分類モデルになります。
分類の場合、2値応答を使用した分析と多項応答を使用した分析に、さらに数学的な詳細を追加できます。
2値応答
モデルの作成では、次の情報を使用します：
- 応答変数、
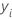、次の値をとります：{-1,
1}.
- 一般化残差の計算の初期適合値は、次の形式で計算されます：
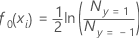
ここで、
はイベントの数と
は非事象の数。
モデルの作成では、アナリストからの次の入力も使用されます：
| 入力 | 記号 |
|---|---|
| 学習率 |  |
| サンプル率 |  |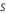
| ツリーあたりの終端ノードの最大数 |  |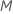
| 木の数 |  |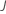
このプロセスには、j番目の木を拡張するための一般的な手順が次に示されています(j=1,...,J)。
- トレーニングデータから s * N のサイズのランダムサンプルを引き出します (N はトレーニングデータ内の行数)。
- gi, jを計算します
,
,
:
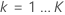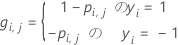
ここで
および
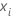は、トレーニングデータ内の予測値の
i番目の行を表すベクトルです。
- 一般化残差に、最大M個のターミナルノードを持つ回帰木を適合します。木は、観測値を最大M個の相互に排他的なグループに分割します。
- 回帰木の
m番目のノードについて、前の木から適合値のノード内の更新を次のように計算します。
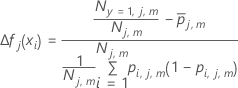ここで、用語 説明 
木jにおけるターミナルノードmの事象数 
木jにおけるターミナルノードmのケース数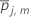 
- ノード内の更新を学習率で縮小し、値を適用して更新された適合値
fj(xi):を取得します：
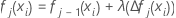
- 分析のJ個の木のそれぞれに対してステップ1から5を繰り返します。
多項応答
K水準の多項応答の場合、分析は各反復で応答変数の各水準に木を適合します。いずれかの木の一般化残差を計算するための初期適合値は、次の形式で計算されます：
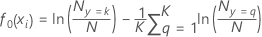
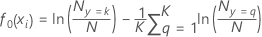
ここで、
は、応答値が
k の場合のケースの数です。Nはトレーニングデータ内の行数です。
モデルの作成では、アナリストからの次の入力も使用されます：
| 入力 | 記号 |
|---|---|
| 学習率 |  |
| サンプル率 |  |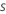
| ツリーあたりの終端ノードの最大数 |  |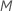
| 木の数 |  |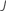
適合値から確率の計算は、これらの木の依存性を表します。それ以外の場合、このプロセスは2値の場合とほぼ同じです。
- トレーニングデータからサイズ s * N のランダムサンプルを描画します (N はトレーニングデータの行数)。
- gi、j、kを計算します:
,
、解析内のツリーの数、および
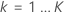、応答変数の水準数
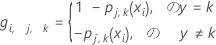
ここで、
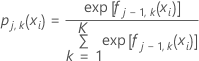
および
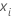は、トレーニングデータセット内の予測値の
i番目の行を表すベクトルです。
たとえば、3水準の多項応答から1としてコード化された結果の確率は、次の形式になります。ここで、
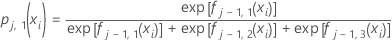
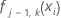は、応答変数のk番目の水準に対するj–1
番目の木のi番目の適合値です。
- 一般化残差に、最大M個のターミナルノードを持つ回帰木を適合します。木は、観測値を最大M個の相互に排他的なグループに分割します。
- j番目の回帰木の
m番目のターミナルノードについて、前の木から適合値のノード内の更新を次のように計算します。
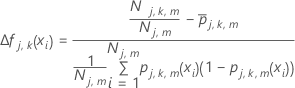
ここで、
用語 説明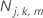 
木jにおけるターミナルノードmの結果kのケース数 
木jにおけるターミナルノードmのケース数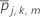 
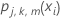木のすべてのケースに対する - ノード内の更新を学習率で縮小し、値を適用して更新された適合値
fj, k, m(xi)を取得します：
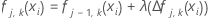
- 分析のJ個の木の数のそれぞれと、応答変数のK個の各水準に対して、ステップ1～5を繰り返します。
