注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
研究チームは、アイオワ州エイムズの個々の居住用不動産の販売データを収集しています。研究者は、販売価格に影響を与える変数を特定したいと考えています。変数には、ロットサイズや居住用不動産のさまざまな特徴が含まれます。
重要な予測変数を特定するためにCART® 回帰で最初の探査を行った後、研究者はRandom Forests® 回帰を使用して同じデータセットからより集約的なモデルを作成します。研究者は、結果のモデル要約表とR2プロットを比較して、どちらが予測精度の高いモデルかを評価します。
これらのデータは、エイムズ住宅データの情報を含む公開データセットに基づいて調整されています。Truman州立大学DeCock教授からのオリジナルデータ。
- サンプルデータエイムズ住宅.MWXを開きます。
- を選択します。
- 応答に「販売価格」を入力します。
- に 'ロット・フロンジ' – '販売年’と入力します連続予測変数。
- に 'タイプ' – '販売条件’と入力しますカテゴリ予測変数。
- オプションをクリックします。
- ノード分割の予測変数の数で、予測変数の総数のKパーセント、K =を選択し、30と入力します。 研究者は、この分析にデフォルトの予測変数より大きな値を使用したいと考えています。
- 各ダイアログボックスのOKをクリックします。
結果を解釈する
方法
| モデル検証 | アウトオブバッグデータを使用した検証 |
|---|---|
| ブートストラップサンプルの数 | 300 |
| サンプルサイズ | 2930のトレーニングデータサイズと同じ |
| ノード分岐に対して選択された予測変数の数 | 予測変数の合計数の30% = 23 |
| 最小内部ノードのサイズ | 5 |
| 使用中の行 | 2930 |
応答情報
| 平均 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|
| 180796 | 79886.7 | 12789 | 129500 | 160000 | 213500 | 755000 |
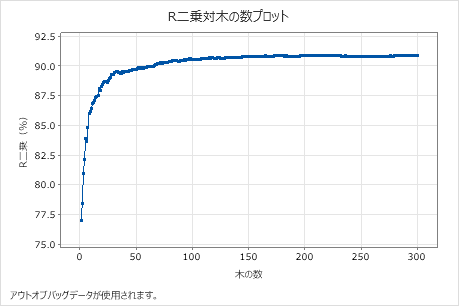
R二乗対木の数プロットは、増加した木の数に対する曲線全体を示します。R2 値は、樹木の数が増えるにつれて急速に増加し、その後約91%で平坦化する。
モデル要約
| 合計予測変数 | 77 |
|---|---|
| 重要な予測変数 | 68 |
| 統計量 | アウトオブバッグ |
|---|---|
| R二乗 | 90.90% |
| 二乗平均平方根誤差(RMSE) | 24097.3281 |
| 平均平方誤差 (MSE) | 5.80681E+08 |
| 平均絶対偏差 (MAD) | 14746.8323 |
| 平均絶対パーセント誤差(MAPE) | 0.0895 |
モデル要約表は、R2値が対応するCART®分析のR2値よりもわずかに改善されていることを示しています。

相対変数重要度グラフは、木のシーケンスに対して予測変数で分岐が行われたときに、モデルの改善に対する予測変数の効果の順に予測変数をプロットします。販売価格を予測するための最も重要な予測変数は品質です。上位の予測変数である品質の重要性が100%の場合、次に重要な変数である居住面積SFの寄与度は88.8%です。これは、生活の平方フィートが物件の全体的な品質と同じくらい88.8%重要であることを意味します。次に重要な変数は、52.6%の寄与度を持つ近傍です。
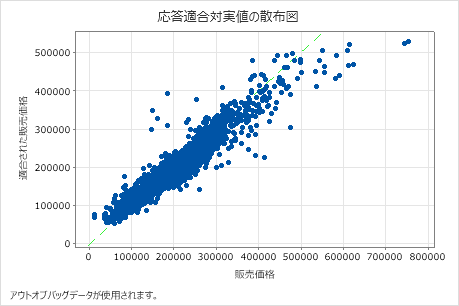
適合された販売金額と実際の販売金額の散布図は、アウトオブバッグデータの適合値と実際の値の関係を示しています。グラフ上のポイントにカーソルを合わせると、プロットされた値をより簡単に確認できます。この例では、多くのポイントが y=x の参照ライン付近に位置しますが、適合値と実測値の間に不一致が見られるために、いくつかのポイントを調査する必要があります。
