注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
重要な変数
Minitab統計ソフトウェアは、変数の重要性をランク付けする2つの方法を提供します。
順列
- A = 87
- B = 9
- C = 4
その行のマージンは 0.87 - 0.09 = 0.78 です。
平均のアウトオブバッグマージンは、すべてのデータ行の平均マージンです。
変数の重要度を判断するには、アウトオブバッグデータ全体で、、xm変数の値をランダムに順序を変えます。応答値と他の予測値は同じままにします。次に、同じステップを使用して、順序を変えたデータの平均マージンを計算します 
.
変数xm の重要度は、2つの平均の差から来ています。
ここで、
は、置換前の平均マージンです。Minitabでは、10–7 未満の値は0に四捨五入されます。
ジニ
分類木は、分岐の集合です。各分岐は、木の改善を提供します。
次の式は、単一のノードでの改善度を示します。
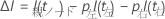
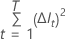
ここで、
は、分割したノードの数と
任意のノード 
ここで、対象の変数はスプリッターではない。
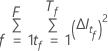
ここで、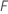
は、フォレスト内の木の数と
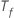はツリーで分割されたノードの数と 
.
ノード不純物の計算は、ジニ法に似ています。ジニ法の詳細については、 におけるノード分岐方法 CART® 分類を参照してください。
平均対数尤度
アウトオブバッグデータ
この計算では、フォレスト内のすべてのツリーのアウトオブバッグサンプルが使用されます。アウトオブバッグサンプルの性質上、データの各行の対数尤度への貢献を見つけるために、異なる木の組み合わせを使用できると予想されます。
フォレスト内の特定のツリーに対して、アウトオブバッグデータの行に対するクラス投票は、単一ツリーの行の予測クラスです。アウトオブバッグデータの行の予測クラスは、フォレスト内のすべてのツリーで最も高い投票数を持つクラスです。アウトオブバッグデータの行の予測クラス確率は、クラスの投票数と行の総投票数の比率です。尤度計算は、次の確率から次のとおりになります。
ここで、
および
は、アウトオブバッグデータの行 i に対して計算された事象確率です。
アウトオブバッグデータの表記
| 用語 | 説明 |
|---|---|
| nOut-of-bag | 1回以上アウトオブバッグである行数 |
| yi, Out-of-bag | アウトオブバッグデータにおけるケース i のバイナリ応答値。事象クラスでは yi, Out-of-bag = 1、それ以外の場合は0。 |
テストセット
フォレスト内の特定のツリーに対して、テストセットの行に対するクラス投票は、単一ツリーの行の予測クラスです。テストセットの行の予測クラスは、フォレスト内のすべてのツリーで最も高い投票数を持つクラスです。テストセットの行の予測クラス確率は、その行に対するクラスの投票数と総投票数の比率です。尤度計算は、次の確率から次のとおりになります。
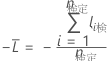
ここで、
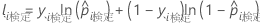
テストセットの表記
| 用語 | 説明 |
|---|---|
| nTest | テストセットのサンプルサイズ |
| yi, Test | テストセットにおけるケース i のバイナリ応答値。事象クラスでは yi, k = 1、それ以外の場合は0。 |
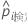 | テストセット内のケース i の予測事象確率 |
ROC曲線下の面積
計算式
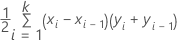
ここで、kは個別の事象確率の数であり、(x0,y0) は点 (0, 0) です。
アウトオブバッグデータまたはテストセットから曲線の面積を計算するには、対応する曲線の点を使用します。
表記
| 用語 | 説明 |
|---|---|
| TPR | 真陽性率 |
| FPR | 偽陽性率 |
| TP | 真陽性、正しく評価された事象 |
| FN | 偽陰性、誤って評価された事象 |
| P | 実際の正の事象の数 |
| FP | 偽陽性、誤って評価された非事象 |
| N | 実際の負の事象の数 |
| FNR | 偽陰性率 |
| TNR | 真陰性率 |
例
| x (偽陽性率) | y (真陽性率) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
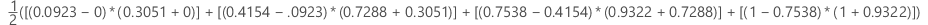
ROC曲線下の面積に対する95%信頼区間
次の区間は、信頼区間の上限と下限を示します。
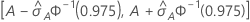
ROC曲線下の面積の標準誤差の計算(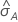
)はSalford Predictive Modeler®からのものです。ROC曲線下の面積の分散の推定に関する一般的な情報は、次の参考資料を参照してください。
Engelmann, B. (2011).Measures of a ratings discriminative power: Applications and limitations.In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer。doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005).Confidence intervals for the area under the ROC curve.Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., & Baumgartner, R. (2017).A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size.Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
表記
| 用語 | 説明 |
|---|---|
| A | ROC曲線下の面積 |
 | 標準正規分布の0.975百分位数 |
リフト
累積リフトの一般的な計算を表示するには、Random Forests® 分類における累積リフトチャートの方法と計算式を参照してください。
誤分類率
次の式は、誤分類率を計算します。
誤分類のカウント数は、予測されたクラスが実際のクラスと異なる場合のアウトオブバッグデータの行数です。合計カウントは、アウトオブバッグデータの行の合計数です。
テストデータセットを使用した検証の場合、誤分類されたカウントは、テストセット内の誤分類の合計です。合計数はテストデータセットに含まれる行数です。
