注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
MARS® 回帰 基本的に、区分線形回帰を当てはめることによって柔軟なモデルを構築します。モデルには、区分線の端点が均等に結合するという制限があります。モデルの非線形性の近似では、データの異なる区間で個別の回帰勾配が使用されます。プロセスの近似は、単純な2次元の場合に簡単に視覚化できます。
2次元の場合、単一の直線がデータに適合します。このモデルは、複雑さの追加の改善をテストするためのベースラインを提供します。
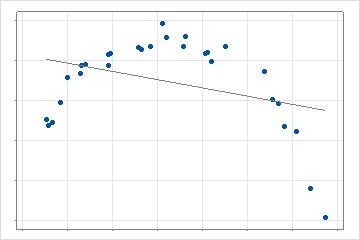
次のステップでは、分析は、検索基準の最大の改善につながる基底関数を作成する予測変数の値を検索します。基準の計算は、分析の選択と検証方法によって異なります。2次元の場合、このモデルは1行ではなく2行の区分線形回帰です。複数の予測変数がある場合、最適なデータポイントの検索では、分析で許可されている各予測変数が評価されます。
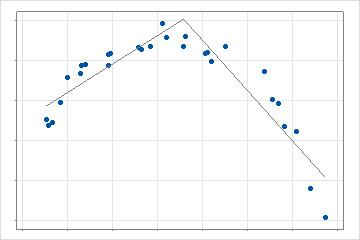
分析では、最適な改善を提供する最初の値が見つかった後、残りの予測変数値が検索され、現在のモデルに対する最適な改善が見つかります。2次元の場合、このモデルにはデータのさまざまな部分を記述する3本の線があります。検索は、分析の基底関数の最大数まで繰り返されます。交互作用が許可されている場合、分析は、候補の基底関数とモデルにすでに存在する他の基底関数を乗算することによって、追加の一連の検索を実行します。
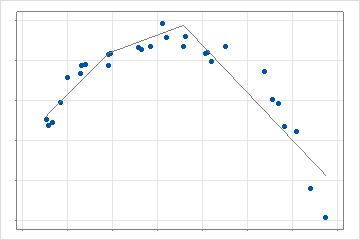
分析が基底関数の最大数にすばやく適合し、それらの関数のパラメータを推定した後、分析によって基底関数の最適な数が特定されます。基底関数の最適数は、段階的後方消去法を使用して、最適性基準の最適値を持つ基底関数の数を見つけます。
モデル適合値の欠損値
基底関数の検索で、 MARS® 回帰 欠損値を持つ予測変数の指標変数を作成します。標識変数は、予測変数の値が欠落しているかどうかを示します。分析にモデルに欠損値を持つ予測変数の基底関数が含まれる場合、モデルには標識変数の基底関数も含まれます。予測変数の他の基底関数はすべて、標識変数の基底関数と相互作用します。
予測変数に欠損値がある場合、標識変数の基底関数は、0 を乗算することによって、その予測変数の他の基底関数を無効にします。欠損値のこれらの基底関数は、重要な予測変数に欠損値があるすべてのモデルにあり、加法モデルや他のタイプの変換を無効にするモデルも含まれます。
予測の欠損値
MARS® 回帰 モデル内の予測変数に欠損値がある場合の予測を計算します。分析では、分析がモデルに適合したときに予測変数の欠損値が存在していたかどうかに応じて、異なる戦略が使用されます。分析がモデルに適合したときに予測変数の欠損値が存在する場合、モデルの基底関数には、予測変数に欠損値があるときにモデルから予測変数を削除する指標変数が含まれます。
2番目のケースは、予測値に予測変数の欠損値が含まれているが、分析がモデルに適合したときに予測変数に欠損値がない場合です。この場合の予測を計算するために、分析は欠損値を代入します。連続予測変数の場合、予測変数の平均によって欠損値が置き換えられます。カテゴリ予測変数の場合、データセット内の最後の非欠損値が欠損値を置き換えます。
