ステップ1:データに対するモデルの適合度を判断します
- テストR二乗
- R2値が高いほど、モデルが良好にデータに適合します。R2 は常に0%と100%の間である。R2はMADに比べ外れ値の影響を受けやすくなります。
- 検定二乗平均平方根誤差 (RMSE)
- 値が小さいほど、適合性が高いことを示します。RMSEはMADに比べ外れ値の影響を受けやすくなります。
- 検定平均二乗誤差 (MSE)
- 値が小さいほど、適合性が高いことを示します。MSEはMADに比べ外れ値の影響を受けやすくなります。
- 検定平均絶対偏差 (MAD)
- 値が小さいほど、適合性が高いことを示します。平均絶対偏差(MAD)は、データと同じ単位で正確性を表し、誤差の量を概念化するのに役立つます。外れ値は、R2、RMSE、およびMSEに対してよりも、MADに対する影響が少ないです。
モデル要約
| 合計予測変数 | 77 |
|---|---|
| 重要な予測変数 | 10 |
| 基底関数の最大数 | 30 |
| 基底関数の最適な数 | 13 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 89.61% | 87.61% |
| 二乗平均平方根誤差(RMSE) | 25836.5197 | 27855.6550 |
| 平均平方誤差 (MSE) | 667525749.7185 | 775937512.8264 |
| 平均絶対偏差 (MAD) | 17506.0038 | 17783.5549 |
主要な結果: 検定 R二乗、検定二乗平均平方根誤差 (RMSE)、検定平均二乗誤差 (MSE)、検定平均絶対偏差 (MAD)
これらの結果では、検定のR二乗は約88%です。検定二乗平均平方根誤差は約27,856です。検定平均の二乗誤差は約775,937,513です。検定平均絶対偏差は約17,784です。
ステップ2:モデルにとって最も重要な変数を特定する
相対変数重要度チャートを使用して、どの予測変数がモデルにとって最も重要な変数であるかを確認します。
重要な変数は、モデル内の少なくとも1つの基底関数にあります。改善度のスコアが最も高い変数が最も重要な変数とされ、他の変数もそれに応じてランク付けされます。相対変数重要度は解釈を容易にするために重要度値が標準化されたものです。相対重要度は、最も重要な予測変数に対するパーセント改善度として定義されます。
相対変数の重要度の値の範囲は 0% から 100% です。最も重要な変数の相対重要度は常に 100% です。変数が基底関数にない場合、その変数は重要ではありません。
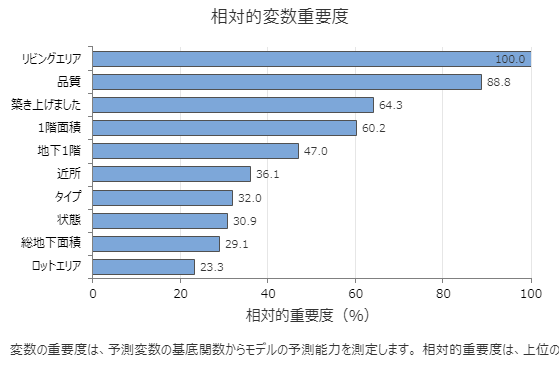
主要な結果: 相対変数重要度
- 品質 は の約 89% が重要です リビングエリア。
- 築き上げました は の約 64% が重要です リビングエリア。
- 1階面積 は の約 60% が重要です リビングエリア。
これらの結果には、確かに重要な10個の変数が含まれますが、相対順位が、特定の応用に関して制御または監視する変数の数に関する情報を提供します。ある変数から次の変数への相対重要度値の急な低下は、どの変数を制御するかまたは監視するかの決定を導くことができます。たとえば、これらのデータでは、2つの最も重要な変数の重要度の値は比較的近く、次の変数に対する相対的な重要度が20%以上低下します。同様に、2つの変数の重要度の値は60%を超えています。さまざまなグループから変数を削除し、分析をやり直して、さまざまなグループの変数がモデル要約表の予測の正確性の値にどのように影響するかを評価できます。
ステップ3:予測変数の効果を調べる
回帰式の偏依存プロット、基底関数、および係数を使用して、予測変数の効果を判断します。予測変数の効果は、予測変数と応答の関係を説明します。応答変数に対する予測変数の効果を理解するために、予測変数のすべての基底関数を検討します。
さらに、他のモデルを構築する際には、重要な予測変数の使用とその関係の形式を考慮してください。たとえば、MARS® 回帰モデルに交互作用が含まれている場合は、それらの交互作用を最小二乗回帰モデルに含めるかどうかを検討して、2 種類のモデルのパフォーマンスを比較します。予測変数を制御するアプリケーションでは、効果によって設定を最適化して応答変数の目標を達成する自然な方法が提供されます。
加法モデルでは、1つの予測変数の偏依存プロットは、重要な連続予測変数が予測応答にどのように影響するかを示します。1つの予測変数の部分依存性プロットは、予測変数レベルの変更に伴って応答がどのように変化すると予想されるか示しています。の場合 MARS® 回帰、プロットの値は、x軸の予測変数の基底関数から取得されます。Y軸の寄与度は、プロット上の最小値が0になるように標準化されています。
主要な結果: 部分依存プロット
このプロットは、 販売価格 データセットの最小平方フィートから約3,000平方フィートに増加するにつれて リビングエリア 増加することを示しています。3,000平方フィートに達すると リビングエリア 、への 販売価格 貢献は約152,000ドルで横ばいになります。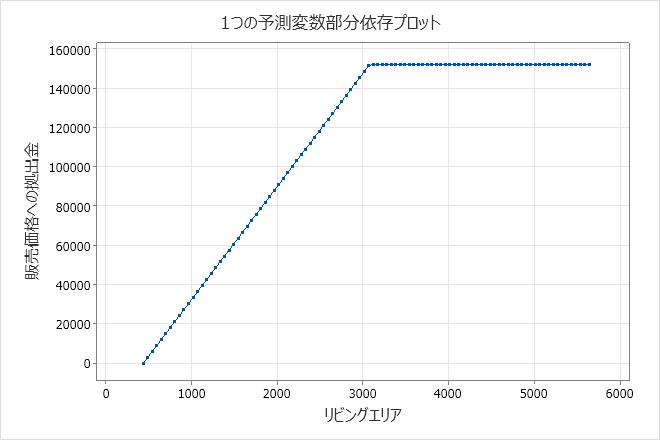
回帰式
BF3=品質が8, 9, 10の場合
BF6=最大(0、2002-築き上げました)
BF7=地下1階が欠落していない場合
BF10=最大(0、1696-地下1階) * BF7
BF11=品質が1, 8の場合
BF13=タイプが90, 150, 160, 180, 190の場合
BF15=近所がヴィーンカー, クリアクリーク, グリーンヒルズ, クロフォード, サマセット・ビレッジズ, ティンバーランド, ノースリッジ, ノースリッジハイツ, ブルーステム, ラ
ンドマーク, 石の橋の場合
BF17=総地下面積が欠落していない場合
BF19=最大(0、総地下面積-1392) * BF17
BF21=最大(0、1階面積-2402)
BF23=状態が1, 2, 3, 4, 5, 6の場合
BF25=品質が1, 7, 10の場合
BF27=最大(0、1階面積-2207)
BF30=最大(0、15138-ロットエリア)
販売価格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
主要な結果: 回帰式
これらの結果では、BF2は回帰式に負の係数を持っています。基底関数の係数は−57.6167です。基底関数の配置は 最大(0, c - X) です。この配置では、予測変数が増加すると基底関数の値は減少します。この配置と負の係数の組み合わせにより、予測変数と応答変数の間に正の関係が作成されます。の リビングエリア 傾きは57.6167で、438から3,078です。
一般的な基底関数のその他の例については、「」を参照してください の回帰式 MARS® 回帰。
