どの程度モデルがデータに適合するかを判断するには、モデル要約表の統計量を調べます。
合計予測変数
モデルで使用可能な合計予測変数の数。これは、指定した連続予測変数とカテゴリ予測変数の総数です。
重要な予測変数
モデル内の重要な予測変数の数。重要な予測変数は、モデル内で少なくとも1つの基底関数を持つ変数です。
解釈
相対変数重要度プロットを使用して、相対変数の重要度の順序を表示することができます。たとえば、20個の予測変数のうち10個がモデルに基底関数を持っているとすると、相対変数重要度プロットには変数が重要度順に表示されます。
基底関数の最大数
最適なモデルを検索するためにアルゴリズムが構築する基底関数の数。
解釈
デフォルトでは、Minitab統計ソフトウェアは基底関数の最大数を30に設定します。30基底関数がデータに対して小さすぎると思われる場合は、より大きな値を検討してください。たとえば、30個を超える予測変数が重要であると思われる場合は、より大きな値を検討します。
基底関数の最適数
最適モデル内の基底関数の数。
解釈
分析で基底関数の最大数を持つモデルを推定した後、分析では逆方向消去法を使用してモデルから基底関数を削除します。分析では、モデルの適合に最も寄与しない基底関数が1つずつ削除されます。各ステップで、分析は分析の最適性基準の値(R2乗または平均絶対偏差)を計算します。消去手順が完了した後の基底関数の最適数は、基準の最適値を生成する消去手順の数です。
R二乗
R2は、モデルによって説明される応答の変動のパーセントです。外れ値は、平均絶対偏差 (MAD) や 平均絶対パーセント誤差 (MAPE) に対してよりも、 R2に大きな影響を与えます。
検証法を使用する場合、表にはトレーニングデータセットのR2統計量とテストデータセットのR2統計量が含まれます。検証法がK分割交差検証の場合、検定データセットはモデルの生成において除外される各分割になります。通常、テストのR2統計量は、新しいデータに対してモデルがどのように働くかについての、優れた指標です。
解釈
R2を使用して、モデルがデータにどの程度適合するかを判断します。R2値が高いほど、モデルが良好にデータに適合します。R2 は常に0%と100%の間である。
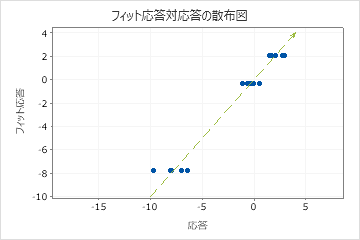
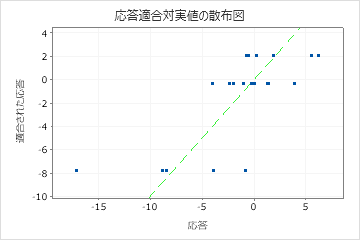
テストR2がトレーニングのR2より大幅に小さい場合は、モデルが現在のデータセットに適合するほどは新しいケースの応答値を予測しない可能性があることを示します。
二乗平均平方根誤差 (RMSE)
二乗平均平方根誤差 (RMSE) は、モデルの正確性を評価します。外れ値は、MADやMAPEに対してよりも、RMSEに大きな影響を与えます。
検証法を使用する場合、表にはトレーニングデータセットのRMSE統計量とテストデータセットのRMSE統計量が含まれます。検証法がK分割交差検証の場合、検定データセットはモデルの生成において除外される各分割になります。通常、テストのRMSE統計量は、新しいデータに対してモデルがどのように働くかについての、優れた指標です。
解釈
さまざまなモデルの適合値を比較するためにを使用します。値が小さいほど、適合性が高いことを示します。テストのRMSEがトレーニングのRMSEより大幅に小さい場合は、モデルが現在のデータセットに適合するほどは新しいケースの応答値を予測しない可能性があることを示します。
平均平方誤差 (MSE)
平均二乗誤差 (MSE) は、モデルの正確性を評価します。外れ値は、MADやMAPEに対してよりも、MSEに大きな影響を与えます。
検証法を使用する場合、表にはトレーニングデータセットの誤差のMSE統計量とテストデータセットのMSE統計量が含まれます。検証法がK分割交差検証の場合、検定データセットはモデルの生成において除外される各分割になります。通常、テストのMSE統計量は、新しいデータに対してモデルがどのように働くかについての、優れた指標です
解釈
さまざまなモデルの適合値を比較するためにを使用します。値が小さいほど、適合性が高いことを示します。テストのMSEがトレーニングのMSEより大幅に小さい場合は、モデルが現在のデータセットに適合するほどは新しいケースの応答値を予測しない可能性があることを示します。
平均絶対偏差 (MAD)
平均絶対偏差(MAD)は、データと同じ単位で正確性を表し、誤差の量を概念化するのに役立つます。外れ値は、R2、RMSE、およびMSEに対してよりも、MADに対する影響が少ないです。
検証法を使用する場合、表には、トレーニングデータセットの MAD統計量とテストデータセットのMAD統計量が含まれます。検証法がK分割交差検証の場合、検定データセットはモデルの生成において除外される各分割になります。通常、テスト MAD統計は、新しいデータに対してモデルがどのように働くかについての、優れた指標です
解釈
さまざまなモデルの適合値を比較するためにを使用します。値が小さいほど、適合性が高いことを示します。テストのMADがトレーニングのMADより大幅に小さい場合は、モデルが現在のデータセットに適合するほどは新しいケースの応答値を予測しない可能性があることを示します。
