注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
研究チームは、アイオワ州エイムズの個々の居住用不動産の販売データを収集しています。研究者は、販売価格に影響を与える変数を特定したいと考えています。変数には、ロットサイズや居住用不動産のさまざまな特徴が含まれます。研究者は、最良のMARS® モデルがデータにどの程度適合するかを評価したいと考えています。
- サンプルデータ、エイムズ住宅.MWXを開きます。
- を選択します。
- 応答に「販売価格」を入力します。
- に 'ロット・フロンジ' – '販売年’と入力します連続予測変数。
- にタイプ – '販売条件’と入力します カテゴリ予測変数。
- OKをクリックします。
結果を解釈する
デフォルトでは、 MARS® 回帰 回帰式のすべての基底関数が1つの予測変数を使用するように加法モデルを適合します。リストの最初の予測変数はBF2です。BF2 は予測変数 リビングエリアを使用します。予測変数は1基底関数であるため、予測変数のモデルには2つの異なる傾きがあります。関数 最大(0, 3078 - リビングエリア) は、居住エリアが 3,078 未満の場合に勾配が 0 以外になることを定義します。
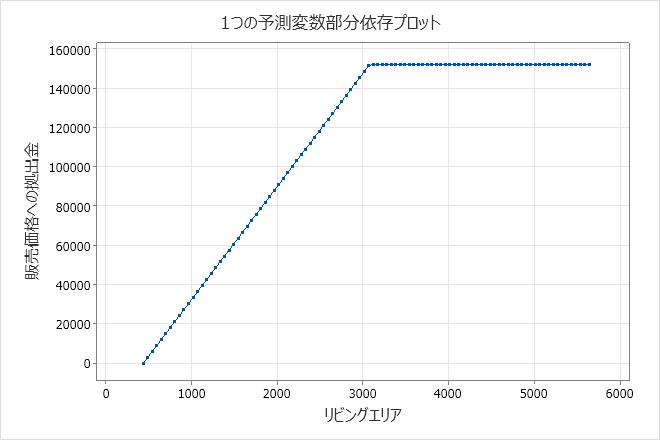
加法モデルの結果には、モデルで重要な連続予測変数の偏依存プロットが含まれます。プロットを使用して、予測変数の範囲全体にわたる予測変数のすべての基底関数の効果を確認します。これらの結果では、偏依存プロットは、438から3,078の値 リビングエリア の場合、傾きが約57.6であることを示しています。が 3,078 より大きい場合 リビングエリア 、傾きは 0 です。
これらの結果では、BF2は回帰式に負の係数を持っています。基底関数の配置は 最大(0, c - X) です。この配置では、予測変数が増加すると基底関数の値は減少します。この配置と負の係数の組み合わせにより、予測変数と応答変数の間に正の関係が作成されます。の影響 リビングエリア は、438から3,078に増加 販売価格 することです。
分析にはカテゴリ予測変数も含まれます。たとえば、BF3 は予測変数 品質用です。基底関数は、の 品質 値が 8、9、または 10 の場合です。式のBF3の係数は115,438です。この基底関数は、品質の値が値 1 から 7 から値 8、9、または 10 に変化すると、モデル内の販売価格が $115,438 増加することを示します。品質 BF11とBF25にもあります。応答変数に対する予測変数の効果を理解するには、すべての基底関数を検討します。
モデルで重要な2つの予測変数には、トレーニングデータに欠損値があります。地下1階 と 総地下面積。基底関数のリストには、これらの予測変数が欠落している場合を識別する基底関数が含まれています。BF7とBF17。予測変数に欠損値がある場合、標識変数の基底関数は、0 を乗算することによって、その予測変数の他の基底関数を無効にします。
回帰式
BF3=品質が8, 9, 10の場合
BF6=最大(0、2002-築き上げました)
BF7=地下1階が欠落していない場合
BF10=最大(0、1696-地下1階) * BF7
BF11=品質が1, 8の場合
BF13=タイプが90, 150, 160, 180, 190の場合
BF15=近所がヴィーンカー, クリアクリーク, グリーンヒルズ, クロフォード, サマセット・ビレッジズ, ティンバーランド, ノースリッジ, ノースリッジハイツ, ブルーステム, ラ
ンドマーク, 石の橋の場合
BF17=総地下面積が欠落していない場合
BF19=最大(0、総地下面積-1392) * BF17
BF21=最大(0、1階面積-2402)
BF23=状態が1, 2, 3, 4, 5, 6の場合
BF25=品質が1, 7, 10の場合
BF27=最大(0、1階面積-2207)
BF30=最大(0、15138-ロットエリア)
販売価格 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
注
これらの結果では、基底関数のリストには15個の基底関数がありますが、基底関数の最適数は13です。回帰式には、13 個の基底関数が含まれています。基底関数のリストには、欠損値を識別する基底関数である BF7 と BF17 が含まれています。これらの基底関数は、検索の他の基底関数ほど MSE を縮小しなかったため、それ自体は重要ではありません。これらの2つの基底関数は、重要なBF10とBF19の完全な計算を示すためにリストにあります。
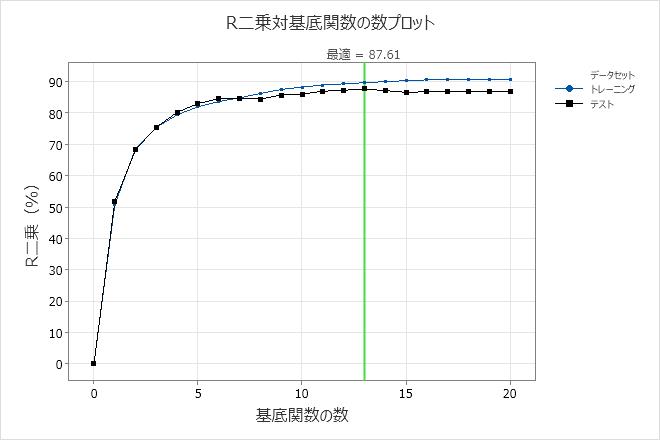
R二乗対基底関数数プロットは、基底関数の最適な数を見つけるための後方消去の結果を示します。基底関数の数が異なるモデルを使用するには、 代替モデルの選択を選択します。たとえば、基底関数がはるかに少ないモデルが最適モデルとほぼ同じ精度である場合は、より単純なモデルを使用するかどうかを検討します。これらの結果では、トレーニングデータセットとテストデータセットのR2乗値は、7つの基底関数を持つモデルで同じです。この小さいモデルは、オーバーフィッティングが懸念される場合に重要です。
モデル要約
| 合計予測変数 | 77 |
|---|---|
| 重要な予測変数 | 10 |
| 基底関数の最大数 | 30 |
| 基底関数の最適な数 | 13 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 89.61% | 87.61% |
| 二乗平均平方根誤差(RMSE) | 25836.5197 | 27855.6550 |
| 平均平方誤差 (MSE) | 667525749.7185 | 775937512.8264 |
| 平均絶対偏差 (MAD) | 17506.0038 | 17783.5549 |
モデルの概要テーブルには、モデルのパフォーマンスの測定値が含まれています。これらの値を使用してモデルを比較できます。これらの結果では、検定のR二乗は約88%です。
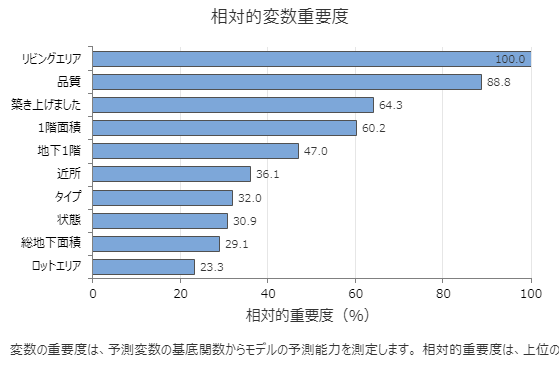
相対変数重要度チャートは、モデルへの影響の順に予測変数をプロットします。最も重要な予測変数はリビングエリアです。最上位の予測変数 リビングエリアの寄与度が 100% の次に重要な変数 品質の寄与度は 88.8% になります。この貢献は、このモデルと同じくらい リビングエリア 88.8%重要であることを意味します 品質 。
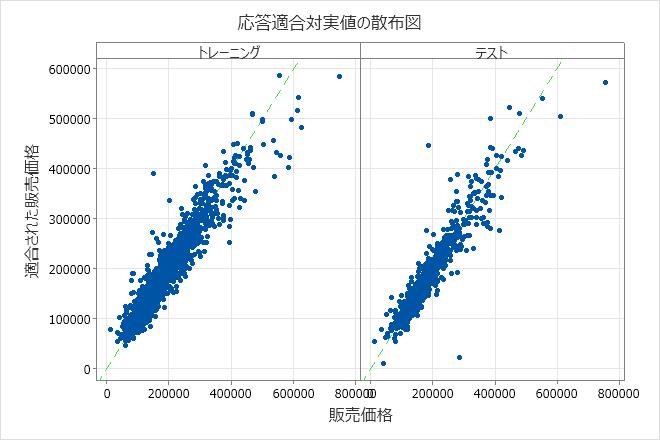
適合販売価格と実際の販売価格の散布図は、トレーニングデータとテストデータの両方の適合値と実際の値の関係を示します。グラフ上のポイントにカーソルを合わせると、プロットされた値をより簡単に確認できます。この例では、ほとんどのポイントが y=x の参照線にほぼ近くにあります。
このモデルは、適合販売価格が100,000ドル未満で実際の販売価格が250,000ドルに近いテストデータセットのモデルなど、いくつかの明確なポイントに不十分に適合しています。モデルの適合度を向上させるために、このケースを調査するかどうかを検討してください。
