注
このコマンドは、予測分析モジュールで使用できます。モジュールをアクティブにする方法については、ここをクリックしてください。
このトピックの内容
最適なタイプのモデルを探す
医療システムの研究者は、地域の診療所からデータを収集します。特に、研究チームは、病気の患者の医師の初期検査からのデータに興味を持っています。最初の検査の最後に、医師は各患者に病気の重症度のスコアを割り当てます。研究者は、医師による検査の前に最も病気の患者に優先順位を付けるのに役立つ短い質問票を作成したいと考えています。対象分野の専門家との協議とデータの初期調査を通じて、チームは重大度スコアを予測するために8つの変数を選択します。研究者は、モデルをさらに改良する前に、重大度スコアを予測するための最適なタイプのモデルを決定したいと考えています。
研究者は、重回帰、TreeNet®、Random Forests® 、CART® 、MARS®の5種類のモデルの予測パフォーマンスを比較するために使用します ベストモデルの検出(連続応答) 。チームは、最高の予測パフォーマンスを備えたモデルのタイプをさらに調査する予定です。
- サンプルデータ、病気.MWXを開きます。
- を選択します。
- 応答に「病気の重症度スコア」を入力します。
- 連続予測変数に「今の症状の数」を入力します。
- に カテゴリ予測変数'痰の高生産'-'通常の活動の制限' と入力します。
- OKをクリックします。
結果を解釈する
モデル選択テーブルでは、モデルの種類のパフォーマンスが比較されます。重回帰モデルの最大値はR2です。以下の結果は、最適な重回帰モデルに対するものです。
モデルにおける応答と各項の間の関係が統計的に有意かどうか判断するには、項のp値と有意水準を比較して帰無仮説を評価します。この帰無仮説は、項と応答に関連性がないという仮定です。通常、0.05の有意水準(αまたはアルファとも呼ばれる)が有効に機能します。0.05の有意水準は、実際の関連性がないのに関連性が存在すると結論付けるリスクが5%であることを示します。これらの結果では、2つの交互作用項のp値が0.05を超えています。息切れの激しさ*激しい頭痛 および 激しい頭痛*重度の睡眠障害。研究者が他の重回帰モデルを探索する場合、モデルのパフォーマンスメトリックと残差プロットを使用して、これらの項をモデルに含めることの影響を調査します。
モデル要約表は、トレーニングR2およびテストR2 が共に約 91%であることを示している。検定二乗平均平方根誤差(RMSE)は、データ値が適合値からどれだけ離れているかを表し、約4です。RMSEは疾患スコアの規模が小さいため、研究者は、少数の質問が患者の優先順位付けに役立つ十分な情報であると楽観視しています。
異常な情報の適合と診断の表には、提案された回帰式にうまく従わないデータポイントが示されています。これらは、完全なデータセットからの適合と診断です。
文字Rは、残差が大きい点を示します。異常なデータ点を調べて、モデルが良好に適合しない予測変数の値を確認します。文字Xは、レバレッジの高いポイントを示します。レバレッジの高いポイントは、他のデータセットと比較して異常な予測変数の組み合わせを持ちます。
大きな残差と高いレバレッジポイントは、潜在的に影響力のあるポイントです。たとえば、影響力のある点を含める、または除外することにより、係数が統計的に有意かどうかが変わることがあります。影響力のある観測値が見つかった場合は、その観測値がデータ入力エラーか測定エラーかを判断します。観測値が誤差でない場合は、観測値が結果にどの程度影響するかを判断します。研究者がモデルをさらに探索すると、観測値の有無にかかわらずモデルを適合させます。次に、係数、p値、R2、およびその他のモデル情報を比較します。影響力のある観測値を削除したときにモデルが大幅に変化する場合は、モデルをさらに調べて、モデルを誤って指定したかどうかを判断します。問題を解決するには、さらに多くのデータを集めることが必要な場合もあります。
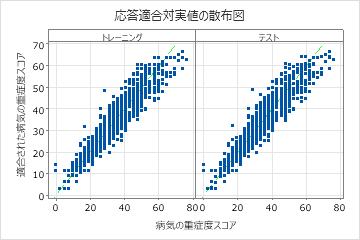
適合された疾患スコアと実際の疾患スコアの散布図は、トレーニングデータとテストデータの両方の適合値と実際の値の関係を示しています。ポイントは y=x の参照線にほぼ近くあり、モデルがデータによく適合していることを示しています。
方法
| 回帰モデルを線形項と2次項で適合させます。 |
|---|
| 平方損失関数を使用して6 TreeNet® 回帰モデルを適合させます。 |
| 1546のトレーニングデータサイズと同じブートストラップサンプルサイズで3 Random Forests® 回帰モデルを適合させます。 |
| 最適なCART®回帰モデルを適合させます。 |
| 最適なMARS®回帰モデルを適合させます。 |
| 5分割のクロス評価から最大R二乗を持つモデルを選択します。 |
| 行の合計数: 1546 |
| 回帰モデルに使用される行: 1546 |
| ツリーベースのモデルに使用される行: 1546 |
応答情報
| 平均 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|
| 31.0110 | 14.0820 | 0 | 19.05 | 30.95 | 40.48 | 76.19 |
| タイプ内のベストモデル | R二乗(%) | 平均絶対偏差 |
|---|---|---|
| 重回帰* | 91.23 | 3.1011 |
| MARS® | 91.05 | 3.1604 |
| TreeNet® | 90.90 | 3.1613 |
| Random Forests® | 89.93 | 3.3248 |
| CART® | 86.11 | 3.9369 |
ベスト重回帰モデルの検証を伴う項の前方選択
*激しい胸痛, 息切れの激しさ*重度の睡眠障害, 一般的に非常に悪い感じ*通常の活動の制限
回帰式
| 病気の重症度スコア | = | 1.241 + 2.5386 今の症状の数 + 0.0 痰の高生産_0 + 3.900 痰の高生産_1 + 0.0 息切れの激しさ_0 + 0.94 息切れの激し さ_1 + 0.0 激しい頭痛_0 + 4.094 激しい頭痛_1 + 0.0 重度の睡眠障害_0 + 3.884 重度の睡眠障害_1 + 0.0 一般的に非常に 悪い感じ_0 + 3.473 一般的に非常に悪い感じ_1 + 0.0 通常の活動の制限_0 + 3.140 通常の活動の制限_1 + 0.0 今の症状の数*息切れ の激しさ_0 + 0.373 今の症状の数*息切れの激しさ_1 + 0.0 今の症状の数*激しい胸痛_0 + 0.4765 今の症状の数*激しい胸痛_1 + 0.0 息切れの激しさ*重度の睡眠障害_0 0 + 0.0 息切れの激しさ*重度の睡眠障害_0 1 + 0.0 息切れの激しさ*重度の睡眠障害_1 0 + 1.337 息切れの激しさ*重度の睡眠障害_1 1 + 0.0 一般的に非常に悪い感じ*通常の活動の制限_0 0 + 0.0 一般的に非常に悪い感じ*通常の活 動の制限_0 1 + 0.0 一般的に非常に悪い感じ*通常の活動の制限_1 0 + 1.372 一般的に非常に悪い感じ*通常の活動の制限_1 1 |
|---|
係数
| 項 | 係数 | 係数の標準誤差 | t値 | p値 | VIF |
|---|---|---|---|---|---|
| 定数 | 1.241 | 0.385 | 3.22 | 0.001 | |
| 今の症状の数 | 2.5386 | 0.0593 | 42.81 | 0.000 | 1.95 |
| 痰の高生産 | |||||
| 1 | 3.900 | 0.225 | 17.35 | 0.000 | 1.10 |
| 息切れの激しさ | |||||
| 1 | 0.94 | 1.18 | 0.80 | 0.424 | 23.23 |
| 激しい頭痛 | |||||
| 1 | 4.094 | 0.253 | 16.18 | 0.000 | 1.25 |
| 重度の睡眠障害 | |||||
| 1 | 3.884 | 0.284 | 13.69 | 0.000 | 1.73 |
| 一般的に非常に悪い感じ | |||||
| 1 | 3.473 | 0.343 | 10.14 | 0.000 | 2.62 |
| 通常の活動の制限 | |||||
| 1 | 3.140 | 0.424 | 7.40 | 0.000 | 3.98 |
| 今の症状の数*息切れの激しさ | |||||
| 1 | 0.373 | 0.133 | 2.81 | 0.005 | 26.80 |
| 今の症状の数*激しい胸痛 | |||||
| 1 | 0.4765 | 0.0312 | 15.26 | 0.000 | 1.25 |
| 息切れの激しさ*重度の睡眠障害 | |||||
| 1 1 | 1.337 | 0.528 | 2.53 | 0.011 | 3.26 |
| 一般的に非常に悪い感じ*通常の活動の制限 | |||||
| 1 1 | 1.372 | 0.527 | 2.61 | 0.009 | 5.73 |
モデル要約
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 91.35% | 91.23% |
| 二乗平均平方根誤差(RMSE) | 4.1562 | 4.1679 |
| 平均平方誤差 (MSE) | 17.2741 | 17.3714 |
| 平均絶対偏差 (MAD) | 3.0798 | 3.1011 |
| R二乗 (調整済み) | 91.29% | |
| R二乗 (予測) | 91.19% |
分散分析
| 要因 | 自由度 | 調整平方和 | 調整平均平方 | F値 | p値 |
|---|---|---|---|---|---|
| 回帰 | 11 | 279881 | 25443.7 | 1472.94 | 0.000 |
| 今の症状の数 | 1 | 31655 | 31654.8 | 1832.51 | 0.000 |
| 痰の高生産 | 1 | 5202 | 5201.8 | 301.14 | 0.000 |
| 息切れの激しさ | 1 | 11 | 11.1 | 0.64 | 0.424 |
| 激しい頭痛 | 1 | 4520 | 4520.0 | 261.66 | 0.000 |
| 重度の睡眠障害 | 1 | 3239 | 3238.8 | 187.50 | 0.000 |
| 一般的に非常に悪い感じ | 1 | 1776 | 1775.6 | 102.79 | 0.000 |
| 通常の活動の制限 | 1 | 945 | 945.4 | 54.73 | 0.000 |
| 今の症状の数*息切れの激しさ | 1 | 136 | 136.4 | 7.90 | 0.005 |
| 今の症状の数*激しい胸痛 | 1 | 4023 | 4023.4 | 232.92 | 0.000 |
| 息切れの激しさ*重度の睡眠障害 | 1 | 111 | 110.7 | 6.41 | 0.011 |
| 一般的に非常に悪い感じ*通常の活動の制限 | 1 | 117 | 117.3 | 6.79 | 0.009 |
| 誤差 | 1534 | 26498 | 17.3 | ||
| 不適合 | 484 | 9247 | 19.1 | 1.16 | 0.025 |
| 純誤差 | 1050 | 17251 | 16.4 | ||
| 合計 | 1545 | 306379 |
異常な観測値の適合値と診断
| 観測値 | 病気の重症度スコア | 適合値 | 残差 | 標準化残差 | ||
|---|---|---|---|---|---|---|
| 11 | 66.670 | 56.757 | 9.913 | 2.40 | R | |
| 13 | 52.380 | 41.177 | 11.203 | 2.71 | R | |
| 16 | 59.520 | 48.604 | 10.916 | 2.64 | R | |
| 33 | 50.000 | 60.657 | -10.657 | -2.57 | R | |
| 48 | 64.290 | 55.416 | 8.874 | 2.14 | R | |
| 52 | 61.900 | 53.369 | 8.531 | 2.06 | R | |
| 54 | 50.000 | 41.598 | 8.402 | 2.03 | R | |
| 56 | 50.000 | 58.328 | -8.328 | -2.02 | R | |
| 58 | 38.100 | 46.485 | -8.385 | -2.03 | R | |
| 106 | 59.520 | 49.028 | 10.492 | 2.53 | R | |
| 114 | 59.520 | 47.160 | 12.360 | 2.99 | R | |
| 128 | 69.050 | 58.328 | 10.722 | 2.59 | R | |
| 144 | 50.000 | 40.471 | 9.529 | 2.30 | R | |
| 173 | 47.620 | 56.757 | -9.137 | -2.21 | R | |
| 174 | 42.860 | 34.000 | 8.860 | 2.14 | R | |
| 191 | 42.860 | 52.051 | -9.191 | -2.23 | R | |
| 198 | 59.520 | 48.411 | 11.109 | 2.68 | R | |
| 202 | 73.810 | 64.046 | 9.764 | 2.36 | R | |
| 205 | 47.620 | 37.559 | 10.061 | 2.43 | R | |
| 213 | 35.710 | 34.970 | 0.740 | 0.18 | X | |
| 217 | 16.670 | 19.053 | -2.383 | -0.58 | X | |
| 239 | 47.620 | 58.328 | -10.708 | -2.59 | R | |
| 241 | 71.430 | 66.311 | 5.119 | 1.25 | X | |
| 243 | 14.290 | 24.088 | -9.798 | -2.36 | R | |
| 304 | 50.000 | 41.130 | 8.870 | 2.14 | R | |
| 307 | 14.290 | 10.920 | 3.370 | 0.83 | X | |
| 352 | 64.290 | 51.254 | 13.036 | 3.15 | R | |
| 369 | 38.100 | 49.275 | -11.175 | -2.70 | R | |
| 391 | 16.670 | 32.073 | -15.403 | -3.72 | R | |
| 392 | 0.000 | 11.395 | -11.395 | -2.75 | R | |
| 395 | 0.000 | 13.934 | -13.934 | -3.36 | R | |
| 424 | 40.480 | 52.504 | -12.024 | -2.90 | R | |
| 425 | 47.620 | 34.597 | 13.023 | 3.16 | R | |
| 474 | 47.620 | 38.538 | 9.082 | 2.21 | R | |
| 479 | 40.480 | 30.896 | 9.584 | 2.31 | R | |
| 489 | 16.670 | 25.023 | -8.353 | -2.02 | R | |
| 491 | 30.950 | 24.348 | 6.602 | 1.61 | X | |
| 493 | 57.140 | 44.339 | 12.801 | 3.09 | R | |
| 495 | 35.710 | 25.480 | 10.230 | 2.47 | R | |
| 509 | 38.100 | 26.696 | 11.404 | 2.77 | R | |
| 520 | 73.810 | 58.328 | 15.482 | 3.75 | R | |
| 537 | 38.100 | 28.358 | 9.742 | 2.35 | R | |
| 550 | 14.290 | 24.458 | -10.168 | -2.45 | R | |
| 583 | 42.860 | 53.369 | -10.509 | -2.54 | R | |
| 694 | 19.050 | 21.817 | -2.767 | -0.68 | X | |
| 720 | 59.520 | 65.602 | -6.082 | -1.49 | X | |
| 722 | 40.480 | 32.066 | 8.414 | 2.03 | R | |
| 802 | 30.950 | 42.586 | -11.636 | -2.81 | R | |
| 805 | 30.950 | 39.868 | -8.918 | -2.16 | R | |
| 814 | 40.480 | 32.073 | 8.407 | 2.03 | R | |
| 823 | 61.900 | 48.148 | 13.752 | 3.33 | R | |
| 833 | 33.330 | 44.054 | -10.724 | -2.60 | R | |
| 859 | 38.100 | 49.275 | -11.175 | -2.70 | R | |
| 868 | 47.620 | 37.789 | 9.831 | 2.38 | R | |
| 891 | 30.950 | 19.945 | 11.005 | 2.66 | R | |
| 893 | 28.570 | 48.860 | -20.290 | -4.92 | R | |
| 905 | 45.240 | 55.416 | -10.176 | -2.46 | R | |
| 924 | 54.760 | 56.019 | -1.259 | -0.31 | X | |
| 977 | 64.290 | 53.107 | 11.183 | 2.72 | R | |
| 983 | 57.140 | 47.683 | 9.457 | 2.29 | R | |
| 988 | 50.000 | 44.501 | 5.499 | 1.34 | X | |
| 993 | 73.810 | 64.046 | 9.764 | 2.36 | R | |
| 997 | 33.330 | 24.458 | 8.872 | 2.14 | R | |
| 1003 | 54.760 | 45.128 | 9.632 | 2.33 | R | |
| 1025 | 33.330 | 47.705 | -14.375 | -3.49 | R | |
| 1059 | 57.140 | 48.663 | 8.477 | 2.05 | R | |
| 1105 | 47.620 | 37.319 | 10.301 | 2.49 | R | |
| 1150 | 59.520 | 44.339 | 15.181 | 3.67 | R | |
| 1160 | 52.380 | 40.051 | 12.329 | 2.97 | R | |
| 1163 | 30.950 | 41.598 | -10.648 | -2.57 | R | |
| 1165 | 69.050 | 56.757 | 12.293 | 2.97 | R | |
| 1169 | 59.520 | 49.275 | 10.245 | 2.48 | R | |
| 1198 | 42.860 | 51.516 | -8.656 | -2.09 | R | |
| 1207 | 76.190 | 63.534 | 12.656 | 3.07 | R | |
| 1213 | 26.190 | 40.278 | -14.088 | -3.41 | R | |
| 1228 | 40.480 | 50.571 | -10.091 | -2.45 | R | |
| 1235 | 59.520 | 50.175 | 9.345 | 2.26 | R | |
| 1237 | 57.140 | 48.239 | 8.901 | 2.15 | R | |
| 1246 | 64.290 | 55.416 | 8.874 | 2.14 | R | |
| 1262 | 45.240 | 35.957 | 9.283 | 2.24 | R | |
| 1263 | 57.140 | 43.951 | 13.189 | 3.18 | R | |
| 1282 | 33.330 | 36.011 | -2.681 | -0.65 | X | |
| 1284 | 45.240 | 56.564 | -11.324 | -2.74 | R | |
| 1285 | 47.620 | 60.657 | -13.037 | -3.15 | R | |
| 1303 | 26.190 | 36.567 | -10.377 | -2.51 | R | |
| 1305 | 35.710 | 45.499 | -9.789 | -2.36 | R | |
| 1311 | 30.950 | 40.089 | -9.139 | -2.21 | R | |
| 1345 | 26.190 | 25.105 | 1.085 | 0.26 | X | |
| 1353 | 42.860 | 53.175 | -10.315 | -2.49 | R | |
| 1365 | 26.190 | 17.834 | 8.356 | 2.01 | R | |
| 1377 | 47.620 | 35.222 | 12.398 | 3.00 | R | |
| 1380 | 69.050 | 55.416 | 13.634 | 3.29 | R | |
| 1384 | 50.000 | 38.496 | 11.504 | 2.78 | R | |
| 1414 | 26.190 | 35.345 | -9.155 | -2.21 | R | |
| 1502 | 61.900 | 50.195 | 11.705 | 2.84 | R | |
| 1526 | 38.100 | 25.450 | 12.650 | 3.05 | R | |
| 1535 | 14.290 | 24.088 | -9.798 | -2.36 | R | |
| 1544 | 38.100 | 29.165 | 8.935 | 2.16 | R | |
| 1548 | 50.000 | 40.455 | 9.545 | 2.31 | R | |
| 1565 | 38.100 | 42.846 | -4.746 | -1.16 | X | |
| 1582 | 66.670 | 55.437 | 11.233 | 2.72 | R |
代替モデルを選択
研究者は、最良のTreeNet® モデルの結果を調べることにしました。
- の結果 ベストモデルの検出(連続応答)で、 を選択します 代替モデルの選択。
- モデルタイプでTreeNet®を選択します。
- で 既存のモデルを選択する、R2の最良の値を持つ6番目のモデルを選択します。
- 結果を表示をクリックします。
結果を解釈する
この分析では 300 本の木が生え、最適な木の数は 63 本です。このモデルでは、学習率 0.1、サブサンプルの割合 0.7 を使用します。ターミナルノードの最大数は 6 です。
方法
| 損失関数 | 二乗誤差 |
|---|---|
| 木の最適な数の選択基準 | 最大R二乗 |
| モデル検証 | 5分割交差検証 |
| 学習率 | 0.1 |
| サブサンプルの割合 | 0.7 |
| 木あたりの最大終端ノード | 6 |
| 最小終端節サイズ | 3 |
| ノード分岐に対して選択された予測変数の数 | 予測変数の合計数 = 8 |
| 使用中の行 | 1546 |
| 未使用の行 | 70 |
応答情報
| 平均 | 標準偏差 | 最小 | Q1 | 中央値 | Q3 | 最大 |
|---|---|---|---|---|---|---|
| 31.0110 | 14.0820 | 0 | 19.05 | 30.95 | 40.48 | 76.19 |
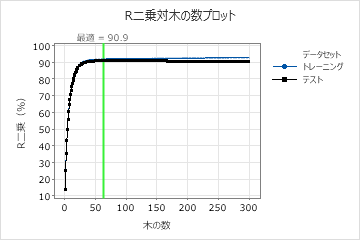
R二乗対木の数プロットは、増加した木の数に対する曲線全体を示します。テストデータの最適値は、木の数が63の場合、約91%です。
モデル要約
| 合計予測変数 | 8 |
|---|---|
| 重要な予測変数 | 8 |
| 増加した木の数 | 300 |
| 最適な木の数 | 63 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| R二乗 | 91.93% | 90.90% |
| 二乗平均平方根誤差(RMSE) | 3.9992 | 4.2471 |
| 平均平方誤差 (MSE) | 15.9932 | 18.0375 |
| 平均絶対偏差 (MAD) | 2.9943 | 3.1613 |
| 平均絶対パーセント誤差(MAPE) | 0.1088 | 0.1130 |
モデル要約表は、木の数が63のときのR2値が、学習データで約92 %、テストデータで約91%であることを示しています。
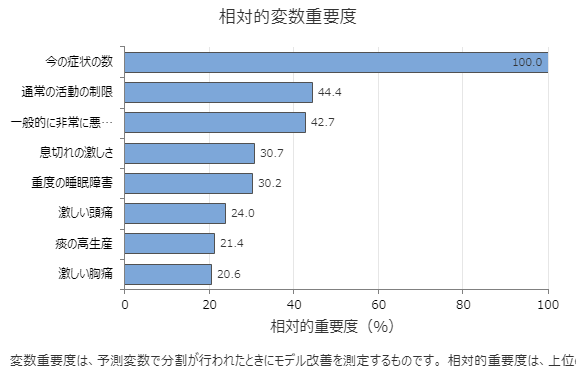
相対変数重要度グラフは、木のシーケンスに対して予測変数で分岐が行われたときに、モデルの改善に対する予測変数の効果の順に予測変数をプロットします。最も重要な予測変数は今の症状の数です。最上位の予測変数 今の症状の数の寄与度が 100% の場合、次に重要な変数 通常の活動の制限の寄与度は 44.4% になります。これは、この回帰モデルと同じくらい 今の症状の数 44.4%重要であることを意味します 通常の活動の制限 。
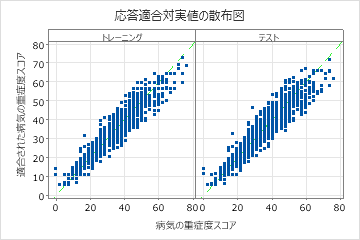
適合された疾患スコアと実際の疾患スコアの散布図は、トレーニングデータとテストデータの両方の適合値と実際の値の関係を示しています。ポイントは y=x の参照線にほぼ近くあり、モデルがデータによく適合していることを示しています。
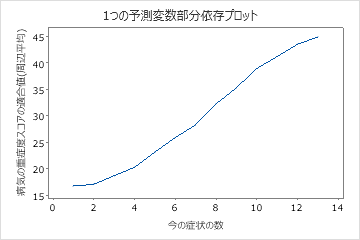
偏依存プロットを使用して、重要な変数または変数のペアが適合応答値にどのように影響するかについての洞察を得ます。部分依存プロットは、応答と変数の関係が線形、単調、またはより複雑であるかどうかを示します。
最初のプロットは、病気のスコアと患者の現在の症状の数との関係を示しています。個々のデータポイントにカーソルを合わせると、特定のx値とy値が表示されます。たとえば、グラフの右側の最高点は、患者に13の症状があり、適合疾患スコアが約45の場合です。
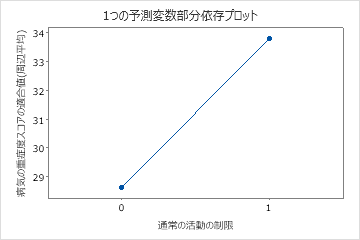
2番目のプロットは、患者が通常の活動の制限を報告すると、適合疾患スコアが約5ポイント増加することを示しています。
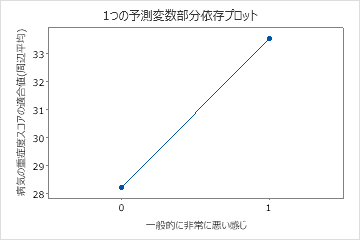
3番目のプロットは、患者が一般的に非常に気分が悪いと報告した場合、適合疾患スコアが約5ポイント増加することを示しています。
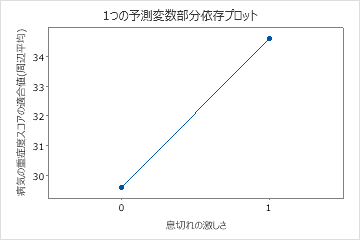
4番目のプロットは、患者が重度の息切れを報告した場合に、適合疾患スコアが約4ポイント増加することを示しています。
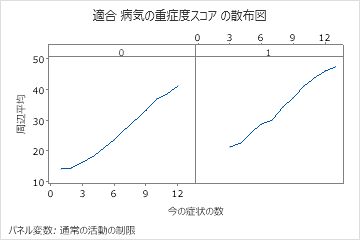
最後のプロットは、多くの症状に対する適合疾患スコアが、患者が通常の活動にも制限があるかどうかにどのように依存するかを示しています。同じ数の症状について、通常の活動の制限も報告している患者は、より高い適合疾患スコアを持っています。
