トレーニングデータセットまたは検証なし
トレーニングデータセットのチャートでは、チャート上の各点は、木のターミナルノードを表します。事象確率が最も高いターミナルノードは、チャート上の最初の点で、左端に表示されます。その他の終端ノードは、事象確率が減少する順序に並んでいます。次の手順に従って、チャートのx座標とy座標を計算します。
- 各ターミナルノードの事象確率を計算します。
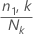
- n1,kはk番目のノードにあるケースの数です。
- Nkはk番目のノードにあるケースの数です。
- 終端ノードを最高の事象確率から最低の事象確率にランク付けします。
- すべての事象確率をしきい値として使用します。ある特定のしきい値に関して、推定された事象確率がしきい値以上の場合は予測クラスとして1となり、それ以外の場合は0となります。次に、観測されたクラスを行とし、予測されたクラスを列として、すべての場合に対して2x2の表を形成し、各ターミナルノードに関連する偽陽性率と真陽性率を計算できます。偽陽性率はチャートのx座標で、真陽性率はy座標です。
たとえば、次の表に、4つのターミナルノードがある木を要約するとします。
A:ターミナルノード B:事象数 C:非事象数 D:ケースの数 E:しきい値 (B/D) 4 18 12 30 0.60 1 25 42 67 0.37 3 12 44 56 0.21 2 4 32 36 0.11 合計 59 130 189 次に、対応する4つの表に、それぞれの偽陽性率および真陽性率を、小数点以下2桁で示します。
表 1. しきい値 = 0.60. 偽陽性率 = 12 / (12 + 118) = 0.09
真陽性率 = 18 / (18 + 41) = 0.31
予測値 事象 非事象 観測 事象 18 41 非事象 12 118 表 2. しきい値 = 0.37. 偽陽性率 = (12 + 42) / 130 = 0.42
真陽性率 = (18 + 25) / 59 = 0.73
予測値 事象 非事象 観測 事象 43 16 非事象 54 76 表 3. しきい値 = 0.21. 偽陽性率 = (12 + 42 + 44) / 130 = 0.75
真陽性率 = (18 + 25 + 12) / 59 = 0.93
予測値 事象 非事象 観測 事象 55 4 非事象 98 32 表 4. しきい値 = 0.11. 偽陽性率 = (12 + 42 + 44 + 32) / 130 = 1
真陽性率 = (18 + 25 + 12 + 4) / 59 = 1
予測値 事象 非事象 観測 事象 59 0 非事象 130 0
別のテストデータセット
トレーニングデータセットの手段と同じ手順を使用しますが、テストデータセットのケースから事象確率を計算します。
K分割交差検証を使用したテスト
K分割交差検証を使用してROC曲線チャート上のx座標とy座標を定義する手順には、追加のステップがあります。このステップにより、多くの異なる事象確率が生成されます。たとえば、ツリー図に4つのターミナルノードがあるとします。私たちは10分割交差検証を行います。次に、i番目の分割で、データの9/10の部分を使用して、分割iのケースの事象確率を推定します。このプロセスを各分割で繰り返す場合、個別の事象確率の最大数は4 *10 = 40です。その後、すべての個別の事象確率を降順に並べ替えます。データセット全体の場合に関して予測クラスを割り当てるには、各しきい値として事象確率を使用します。この手順の後、トレーニングデータセットの3から最後までのステップを適用し、x座標とy座標を計算します。
