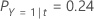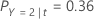分類木は、元のトレーニングデータセットの2値の再帰的な分割の結果として生成されます。木の親ノード(トレーニングデータのサブセット)は、ノードで収集された実際のデータ値に応じて、有限の方法で2つの相互排他的な子ノードに分岐できます。
分岐手順では、予測変数を連続またはカテゴリーとして扱います。連続変数がXで、ある値cの場合、分岐は、Xの値がc以下の記録をすべて左のノードに送り、残りのすべての記録を右のノードに送ることによって定義されます。CARTは、cを計算するために、隣接する2つの値の平均を常に使用します。N個の個別な値をもつ連続変数は、親ノードのN –1個の可能性がある分岐を生成します(最小許容ノードサイズの制限が課されると、実際の数は小さくなります)。
たとえば、ある連続予測変数は、データ値55、66、および75をもちます。この変数の分岐の1つとして、(55+66)/2 = 60.5未満の値をすべて1つの子ノードに、60.5より大きいすべての値をもう一方の子ノードに送る場合があります。予測変数が55のケースは1つのノードに、値66と75のケースは他のノードに移動します。この予測変数のもう 1つの分岐は、70.5以下のすべての値を1つの子ノードに、70.5より大きい値をもう一方のノードに送るというものです。値が55および66のケースは1つのノードに、値が75のケースは他のノードに移動します。
個別の値 {c1, c2 ..., ck} をもつカテゴリ変数Xの場合、分岐は左の子ノードに送られる水準のサブセットとして定義されます。K個の水準をもつカテゴリ変数は、最大2K-1–1個の分岐を生成します。
| 左の子ノード | 右の子ノード |
|---|---|
| 赤、 青 | 黄色 |
| 赤、 黄色 | 青 |
| 青、 黄色 | 赤 |
分類木では、目的変数はKの個別クラスがある多項です。木の目的は、できる限り純度が高くなる方法で、異なる目的変数のクラスを個々のノードに分類する方法を見つけることです。結果として得られるターミナルノードの数はK個である必要はありません。多様なターミナルノードを使用して、特定の目的変数のクラスを表すことができます。ユーザーは、目的変数のクラスの事前確率を指定できます。これらは木の成長プロセス中にCARTによって考慮されます。
次のセクションでは、2値応答変数に対して次の定義が使用されます。
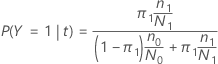
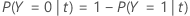
次のセクションでは、多項応答変数に対して次の定義が使用されます。
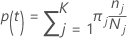
ノードtのクラスjの確率:
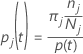
これらの定義は、ノード内の確率を与えます。Minitabでは、すべてのノードとすべての可能な分岐に対してこれらの確率が計算されます。Minitabでは、次のいずれかの基準を使用して、これらの確率から、可能な分岐に対する全体的な改善度が計算されます。
表記
| 用語 | 説明 |
|---|---|
| K | number of classes in the response variable |
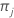 | prior probability for class j |
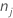 | number of observations for class j in a node |
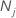 | number of observations for class j in the data |
ジニ基準
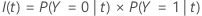
次の、より一般的な計算式は、多項応答変数に適用されます。
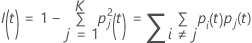
ノードのすべての観測値が1つのクラスに含まれている場合、  となることに注意してください。
となることに注意してください。
エントロピー基準

次の、より一般的な計算式は、多項応答変数に適用されます。
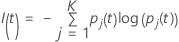
ノードのすべての観測値が1つのクラスに含まれている場合、  となることに注意してください。
となることに注意してください。
Twoing基準
| スーパークラス1 | スーパークラス2 |
|---|---|
| 1, 2, 3 | 4 |
| 1, 2, 3 | 3 |
| 1, 3, 4 | 2 |
| 2, 3, 4 | 1 |
| 1, 2 | 3, 4 |
| 1, 3 | 2, 4 |
| 1, 4 | 2, 3 |
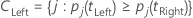
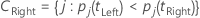
左のスーパークラスには、左に行く傾向があるすべての目的変数のクラスがあります。右のスーパークラスには、右に行く傾向があるすべての目的変数のクラスがあります。
| クラス | 左の子ノードの確率 | 右子ノードの確率 |
|---|---|---|
| 1 | 0.67 | 0.33 |
| 2 | 0.82 | 0.18 |
| 3 | 0.23 | 0.77 |
| 4 | 0.89 | 0.11 |
そして、候補となる分岐のスーパークラスを生成する最良の方法は、1つのスーパー クラスとして {1, 2, 4} を割り当て、もう1つのスーパークラスとして{ 3 }を割り当てるというものです。
残りの計算は、2値の目的変数としてスーパークラスがあるGini基準の場合と同じです。
基準の改善度の計算
Minitabがノードの不純度を計算した後、ある予測変数でノードを分岐する場合の条件付き確率を計算します。
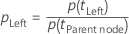
および

そして、分岐の改善度は、次式からのものです。

最高の改善値を持つ分割は、ツリーの一部になります。2 つの予測変数の改善が同じである場合、アルゴリズムを続行するには選択が必要です。選択では、ワークシート内の予測変数の位置、予測変数のタイプ、およびカテゴリ予測変数のクラス数を含む確定的な結合スキームが使用されます。
クラス確率
ノードの分岐は、与えられたノード内のあるクラス確率を最大化します。
ターミナルノード
- ノード内のケースの数がその分析の最小サイズに達しました。Minitab統計ソフトウェアのデフォルトの最小値は3です。
- ノード内のすべてのケースが、同じ応答変数のクラスです。
- ノード内のすべてのケースが、同じ予測変数の値です。
ターミナルノードの予測されたクラス
ターミナルノードの予測されたクラスは、ノードの誤分類コストを最小にするクラスです。誤分類コストの表示は、応答変数のクラス数によって異なります。検証法を使用する場合、ターミナルノードの予測されたクラスはトレーニングデータから得られるため、次のすべての計算式でトレーニングデータセットの確率が使用されます。
2値応答変数
次式は、ノード内のケースが事象のクラスであるという予測の誤分類コストを示します。

次式は、ノード内のケースが非事象のクラスであるという予測の誤分類コストを示します。

| 用語 | 説明 |
|---|---|
| PY=0|t | conditional probability that a case in node t belongs to the non-event class |
| C1|0 | misclassification cost that a nonevent class case is predicted as an event class case |
| PY=1|t | conditional probability that a case in node t belongs to the event class |
| C0|1 | misclassification cost that an event class case is predicted as a nonevent class case |
ターミナルノードの予測されたクラスは、誤分類コストが最小のクラスです。
多項応答変数

たとえば、3つのクラスと次の誤分類コストをもつ応答変数を考えます。
| 予測されたクラス | |||
| 実際のクラス | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
次に、応答変数のクラスがノードtに関して次の確率をもつことを考えます。
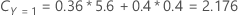


誤分類コストが最も低いのは、Y = 3、 1.164 という予測です。このクラスが、ターミナルノードの予測クラスです。