重要な予測変数
分類木は、分岐の集合です。各分岐は、木の改善を提供します。各分岐には、木の改善を提供する代理変数も含まれます。木が変数を使用してノードを分岐したり、別の変数に欠損値がある場合にノードを分岐する代理変数としてある変数を使用する場合、すべての改善度によって変数の重要性が与えられます。
次の式は、単一のノードでの改善度を示します。
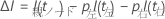
I(t)、pLeft、および pRightの値は、ノードを分割するための基準によって異なります。詳細については、におけるノード分岐方法 CART® 分類を参照してください。
平均対数尤度
トレーニングデータまたは検証なし
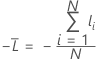
ここで、
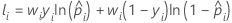
トレーニングデータまたは検証なしの場合の表記
| 用語 | 説明 |
|---|---|
| N | 完全なデータまたはトレーニングデータのサンプルサイズ |
| wi | 完全なデータセットまたはトレーニングデータセット内のi番目の観測の重み |
| yi | 事象の場合は1、それ以外の完全またはトレーニングデータセットの場合は0の指標変数 |
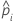 | 完全なデータセットまたはトレーニングデータセット内のi番目の行の事象の予測確率 |
K分割交差検証
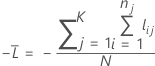
ここで、
K分割交差検証の表記
| 用語 | 説明 |
|---|---|
| N | 完全なデータまたはトレーニングデータのサンプルサイズ |
| nj | 分割jのサンプルサイズ |
| wij | 分割jのi番目の観測値の重み |
| yij | 事象の場合は1、分割jのデータに対しては0の指標変数 |
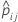 | 分割jのi番目の観測値を含まないモデル推定から事象の予測確率 |
テストデータセット
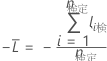
ここで、
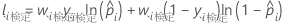
テストデータセットの表記
| 用語 | 説明 |
|---|---|
| nTest | テストセットのサンプルサイズ |
| wi, Test | テストデータセット内のi番目の観測値の重み |
| yi, Test | 事象の場合は1、それ以外はテストセット内のデータに対して0の指標変数 |
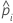 | テストセット内のi番目の行の事象の予測確率 |
ROC曲線下の面積
計算式
曲線下の面積には、積分が使用されます。
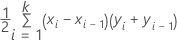
ここで、kはターミナルノードの数、(x0, y0) は点 (0, 0) です。
| x (偽陽性率) | y (真陽性率) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
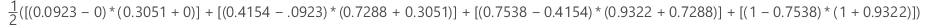
表記
| 用語 | 説明 |
|---|---|
| TRP | 真陽性率 |
| FPR | 偽陽性率 |
| TP | 真陽性、正しく評価された事象 |
| P | 実際の正の事象の数 |
| FP | 真陰性、正しく評価された非事象 |
| N | 実際の負の事象の数 |
| FNR | 偽陰性率 |
| TNR | 真陰性率 |
ROC曲線下の面積に対する95%信頼区間
次の区間は、信頼区間の上限と下限を示します。
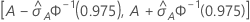
ROC曲線下の面積の標準誤差の計算(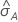
)はSalford Predictive Modeler®からのものです。ROC曲線下の面積の分散の推定に関する一般的な情報は、次の参考資料を参照してください。
Engelmann, B. (2011).Measures of a ratings discriminative power: Applications and limitations.In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer。doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005).Confidence intervals for the area under the ROC curve.Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., & Baumgartner, R. (2017).A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size.Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
表記
| 用語 | 説明 |
|---|---|
| A | ROC曲線下の面積 |
 | 標準正規分布の0.975百分位数 |
リフト
計算式
事象のクラスに割り当てられる確率が最も高いデータの観測値の10%については、次の式を使用します。
テストデータセットのテストリフトの場合は、テストデータセットからの観測値を使用します。K分割交差検証を使用するテストリフトの場合、使用するデータを選択し、モデル推定に含まれていないデータの予測確率からリフトを計算します。
表記
| 用語 | 説明 |
|---|---|
| d | データの10%のケース数 |
 | 事象の予測確率 |
 | トレーニングデータ内の事象の確率、または分析で検証が使用されていない場合は、完全なデータセット内 |
誤分類コスト
モデル要約表の誤分類コストは、すべての観測値を最も頻度が高いクラスに分類する単純な分類器に対する、モデルの相対誤分類コストです。
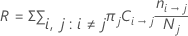
相対誤分類コストは、次の形式になります。
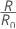
ここでR0 は、単純な分類器のコストです。
Rの計算式は、事前確率が等しい場合、またはデータから得られている場合に単純化されます。
等しい事前確率
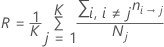
データからの事前確率
この定義では、Rは次の形式になります。
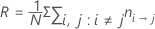
表記
| 用語 | 説明 |
|---|---|
| πj | 応答変数のj番目のクラスの事前確率 |
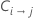 | クラスiクラスjとして誤分類するコスト |
 | クラスjとして誤分類されたクラスiのレコードの数 |
| Nj | 応答変数のj番目のクラスのケースの数 |
| K | 応答変数のクラス数 |
| N | データに含まれるケースの数 |
