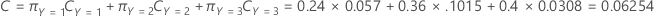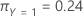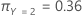分割方法がクラス確率の場合、誤分類の表はありません。
カウント数
重みがない場合、カウント数とサンプルサイズは同じです。
重み付きカウント
重み付きの場合、重み付きカウント数はあるカテゴリの重みの合計です。重み付きカウントとは直近の整数に四捨五入します。パーセンテージとレートを計算するには四捨五入しない重みを使用します。次の単純な例を考えてみます。
| 応答レベル | 予測レベル | 体重 |
|---|---|---|
| はい | はい | 0.1 |
| はい | はい | 0.2 |
| はい | いいえ | 0.3 |
| はい | いいえ | 0.4 |
| いいえ | いいえ | 0.5 |
| いいえ | いいえ | 0.6 |
| いいえ | はい | 0.7 |
| いいえ | はい | 0.8 |
次の表に、次の統計情報を示します:
| 実際のクラス | 重み付きカウント | 誤分類 | 予測クラス = いいえ | 正解率 |
|---|---|---|---|---|
| はい | 0.1 + 0.2 + 0.3 + 0.4 = 1 | 0.1 + 0.2 = 0.3 ≈ 0 | 0.3 + 0.4 = 0.7 ≈ 1 | (0.3 / 1.0) ×100 = 30% |
| いいえ | 0.5 + 0.6 + 0.7 + 0.8 = 2.6 ≈ 3 | 0.7 + 0.8 = 1.5 ≈ 2 | 0.5 + 0.6 = 1.1 ≈ 1 | 1.1 / 2.6) × 100 = 42.31% |
| すべて | 1 + 2.6 = 3.6 ≈ 4 | 0.3 + 1.5 = 1.8 ≈ 2 | 0.7 + 1.1 = 1.8 ≈ 2 | (0.3 + 1.1) / 3.6 × 100 = 38.89% |
%不正解
重み付きの場合、カウント数の代わりに重み付きカウント数を使用します。
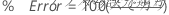
コスト
コストの計算は、応答変数が2値であるか多項であるかによって異なります。
コスト = (%不正解 × クラスの入力誤分類コスト) / 100
2値応答変数
次式は、事象のクラスのコストを示します。

次式は、非事象のクラスのコストを示します。

次式は、すべてのクラスの全体的なコストを示します。

多項応答変数
多項の場合、この式は、可能性がある誤分類のすべてのタイプを考慮して、2値応答変数の数式を拡張します。たとえば、k個のクラスをもつ多項応答の場合、Y = 1の誤分類コストについては次式を使用します。
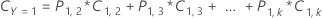
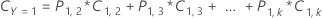
次式は、多項式の場合の全体的なコストを示します。

たとえば、3つのクラスと次の誤分類コストをもつ応答変数を考えます。
| 予測されたクラス | |||
| 実際のクラス | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
次に、次の表に不正解のパーセントを示す値を示します。
| 予測されたクラス | |||
| 実際のクラス | 1 | 2 | 3 |
| 1 | 該当なし | 1% | 0.5% |
| 2 | 1.4% | 該当なし | 2.1% |
| 3 | 5% | 1.2% | 該当なし |
最後に、応答変数のクラスには、以下の事前確率があるとします。
次式は、応答変数の各クラスの誤分類に関連するコストを示します。






次の式は、全体のコストを示します。