ステップ1:代替木を調べる
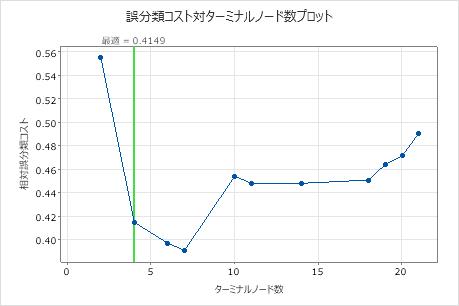
誤分類コスト対ターミナルノード数のプロットには、最適な木が生成される順序で各木の誤分類コストが表示されます。デフォルトでは、最初の最適な木は、誤分類コストが最小な木の1標準誤差内の最小の木です。分析で交差検証またはテストデータセットを使用する場合、誤分類コストは検証サンプルから得られされます。検証サンプルの誤分類コストは、通常、木のサイズが大きくなるにつれて平坦になり、最終的には増加します。
- 最適な木は、誤分類コストが減少しているパターンの一部にあります。さらにいくつかのノードがある1本以上の木が同じパターンの一部にあります。通常、できるだけ予測の正確性が高い木から予測を行う必要があります。木が単純な場合、各予測変数が応答値にどのように影響するかを理解するために使用することもできます。
- 最適な木は、誤分類コストが比較的平坦なパターンの一部にあります。モデルの要約統計量が類似している1本以上の木で、最適な木よりもノード数が非常に少なくなります。通常、ターミナルノードがより少ない木で、各予測変数が応答値にどのように影響するかを明確に把握できます。より小さい木を使用すると、さらに調査を行うために、対象となるいくつかのグループを簡単に特定することもできます。より小さい木の予測の正確性の差がごくわずかである場合は、小さい木を使用して応答と予測変数の関係を評価することもできます。
モデル要約
| 合計予測変数 | 13 |
|---|---|
| 重要な予測変数 | 13 |
| ターミナルノード数 | 4 |
| 最小終端節サイズ | 27 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| 負の対数尤度の平均 | 0.4772 | 0.5164 |
| ROC曲線下面積 | 0.8192 | 0.8001 |
| 95%信頼区間 | (0.3438, 1) | (0.7482, 0.8520) |
| リフト | 1.6189 | 1.8849 |
| 誤分類コスト | 0.3856 | 0.4149 |
主要な結果: 4つのノードがある木のプロットとモデルの要約
4つのノードがある一連の結果の木の誤分類コストは0.41に近くなります。誤分類コストが減少するパターンは、4つのノードの木の後に続きます。このような場合、分析者は、誤分類コストが低い他のいくつかの単純な木を探すことを選択します。
モデル要約
| 合計予測変数 | 13 |
|---|---|
| 重要な予測変数 | 13 |
| ターミナルノード数 | 7 |
| 最小終端節サイズ | 5 |
| 統計量 | トレーニング | テスト |
|---|---|---|
| 負の対数尤度の平均 | 0.3971 | 0.5094 |
| ROC曲線下面積 | 0.8861 | 0.8200 |
| 95%信頼区間 | (0.5590, 1) | (0.7702, 0.8697) |
| リフト | 1.9376 | 1.8165 |
| 誤分類コスト | 0.2924 | 0.3909 |
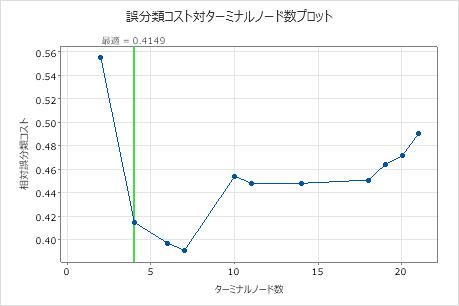
主要な結果: 7つのノードがある木のプロットとモデルの要約
相対的な交差検証の誤分類コストが最小な分類木には、7つのターミナルノードがあり、相対誤分類コストは約0.39です。また、ROC曲線下の面積などの他の統計量も、7つのノードの木が4つのノードの木よりも優れたパフォーマンスを発揮することを裏付けします。7つのノードの木は、解釈しやすい、十分な少数のノードがあるので、分析者は7つのノードの木を使用して、重要な変数を調査し、予測を行うことにします。
ステップ2:ツリー図で最も純度が高いターミナルノードを調べる
ある木を選択した後、図上の最も純度が高いターミナルノードを調べます。青は事象の水準を表し、赤は非事象の水準を表します。
注
ツリー図を右クリックすると、木のノード分岐ビューが表示されます。このビューは、大きな木で、どの変数がノードを分岐するかのみを確認する必要がある場合に有用です。
ノードは、ターミナルノードをそれ以上のグループに分岐できなくなるまで、分岐を続けます。ほとんどが青色のノードは、事象の水準の割合が高いことを示します。ほとんどが赤色のノード場合は、非事象の水準の割合が高いことを示します。
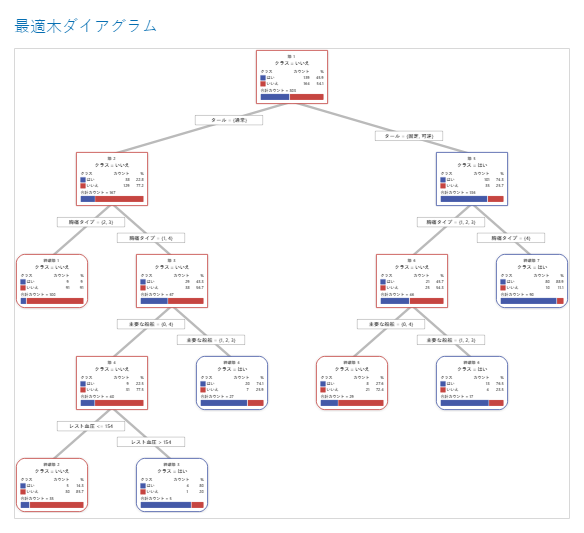
主要な結果: ツリー図
この分類木には7つのターミナルノードがあります。青は事象の水準(はい)、赤は非事象の水準(いいえ)です。このツリー図は、トレーニングデータセットを使用しています。詳細ビューとノード分岐ビューの間で、木のビューを切り替えることができます。
- ノード2: THALは167のケースで正常でした。167のケースのうち、38ケースつまり22.8%が「はい」、129ケースつまり77.2%は「いいえ」です。
- ノード5: THALは136ケースで固定性または可逆性でした。136のケースのうち、101ケースつまり74.3%が「はい」、35ケースつまり25.7%は「いいえ」です。
左の子ノードと右の子ノードの次の分岐変数は、胸痛のタイプで、痛みは 1、2、3、または4で評価されます。ノード2は、ターミナルノード1の親であり、ノード5はターミナルノード7 の親です。
- ターミナルノード1: 100のケースが、THALは正常であり、胸痛は2または3でした。100のケースのうち、9ケースつまり9%が「はい」、91ケースつまり91%は「いいえ」です。
- ターミナルノード7: 90ケースが、THALは固定性または可逆性であり、胸痛は4でした。90のケースのうち、80ケースつまり88.9%が「はい」、10ケースつまり11.1%は「いいえ」です。
ステップ3:重要な変数を決定する
相対変数重要度グラフを使用して、木にとって最も重要な変数である予測変数を特定します。
重要な変数は、木の最良の分岐変数または代理変数です。改善度のスコアが最も高い変数が最も重要な変数とされ、他の変数もそれに応じてランク付けされます。相対変数重要度は解釈を容易にするために重要度値が標準化されたものです。相対重要度は、最も重要な予測変数に対するパーセント改善度として定義されます。
相対変数重要度値の範囲は0%から100%です。最も重要な変数の相対重要度は、常に100%です。ある変数が木でまったく使用されない場合、その変数は重要ではありません。
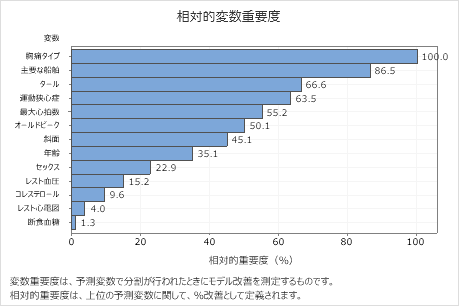
主要な結果: 相対変数重要度
- 主要な船舶 は、約87%が重要です 胸痛タイプ。
- タール と 運動狭心症 、どちらも約 65% 重要です 胸痛タイプ。
- 最大心拍数 は、約55%が重要です 胸痛タイプ。
- オールドピーク は、約50%が重要です 胸痛タイプ。
- 斜面、 年齢、、 セックス、 は レスト血圧 よりも重要 胸痛タイプ度がはるかに低いです。
これらは正の重要性を持っていますが、アナリストは、 、 が コレステロール, レスト心電図, 断食血糖 ツリーの重要な貢献者ではないと判断 する場合があります。
ステップ4:木の予測能力を評価する
最も正確な木は、誤分類コストが最も低い木です。場合によっては、誤分類コストがやや高い、より単純な木も同様に機能します。誤分類コスト対ターミナルノードのプロットを使用して、代替の木を識別することができます。
受信者動作特性 (ROC) 曲線は、木がデータをどの程度良好に分類しているかを示します。ROC曲線は、y軸上に真陽性率、x軸上に偽陽性率をプロットします。真陽性率は、検出力とも呼ばれます。偽陽性率は第1種の過誤とも呼ばれます。
分類木で応答変数のカテゴリを完全に分離できる場合、ROC曲線下の面積は 1となり、これが最良の分類モデルになります。あるいは、分類木でカテゴリを区別できず、分類が完全にランダムに行われた場合、ROC曲線下の面積は0.5になります。
ある手法を使用して木を構築すると、Minitabはトレーニングデータと検証(テスト)データの木のパフォーマンスに関する情報を提供します。これらの曲線が近い場合、木が過剰適合していないことをより確実に確認できます。テストデータの木のパフォーマンスは、木がどの程度良好に新しいデータを予測できるかを示します。
- 真陽性率 (TPR) — 事象のケースが正しく予測される確率
- 偽陽性率 (FPR) — 非事象のケースが誤って予測される確率
- 偽陰性率 (FNR) — 事象のケースが誤って予測される確率
- 真陰性率 (TNR) — 非事象のケースが正しく予測される確率
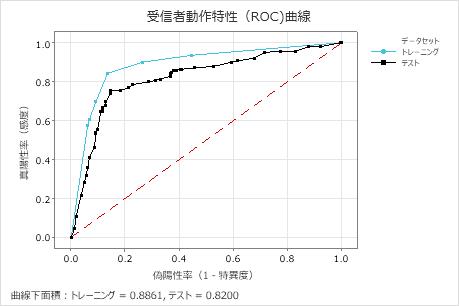
主要な結果: 受信者動作特性 (ROC) 曲線
この例では、ROC曲線下の面積は、トレーニングの場合は0.886、テストでは0.82です。これらの値は、ほとんどの応用で、この分類木が妥当な分類器であることを示しています。
混同行列
| 予測クラス(トレーニング) | 予測クラス(テスト) | ||||||
|---|---|---|---|---|---|---|---|
| 実クラス | 計数 | はい | いいえ | %正 | はい | いいえ | %正 |
| はい (事象) | 139 | 117 | 22 | 84.2 | 105 | 34 | 75.5 |
| いいえ | 164 | 22 | 142 | 86.6 | 24 | 140 | 85.4 |
| すべて | 303 | 139 | 164 | 85.5 | 129 | 174 | 80.9 |
| 統計量 | トレーニング(%) | テスト(%) |
|---|---|---|
| 真陽性率(感度または検出力) | 84.2 | 75.5 |
| 偽陽性率(第一種過誤) | 13.4 | 14.6 |
| 偽陰性率(第二種過誤) | 15.8 | 24.5 |
| 真陰性率(特異度) | 86.6 | 85.4 |
主要な結果: 混同行列
- 真陽性率 (TPR) — トレーニングデータの場合は84.2%、テストデータの場合は75.5%
- 偽陽性率 (FPR) — トレーニングデータの場合は13.4%、テストデータの場合は14.6%
- 偽陰性率 (FNR) — トレーニングデータの場合は15.8%、テストデータの場合は24.5%
- 真陰性率(TNR) — トレーニングデータの場合は86.6%、テストデータの場合は85.4%
全体として、トレーニングデータの%正解は85.5%で、 テストデータの場合は80.9%です。
