事後確率とは、所定のデータの下で、観測値が各グループに割り当てられる確率です。事前確率とは、データを収集する前に観測値がグループ内に収まる確率です。たとえば、特定の車の購入者を分類する場合に、購入者の60%が男性で、40%が女性であることがすでにわかっている可能性があります。このような確率がわかっている場合や推定できる場合、判別分析では、事後確率の計算に、これらの事前確率を使用できます。事前確率を指定しない場合、Minitabではすべてのグループが均一であると仮定されます。
データに正規分布があると仮定して、線形判別関数はln(pi)ずつ増加します(piはグループiの事前確率)。観測値は、最小の一般化距離、つまり最大の線形判別関数に従ってグループに割り当てられるため、その効果により、事前確率が高いグループの事後確率は増加します。
注
事前確率を指定すると、結果の正確性に大きく影響することがあります。グループ間で不等な比率が真の母集団の実際の差を示すかどうか、またはその差がサンプリング誤差によるものかどうかを調べます。
ここで、事前確率があり、fi(x)がグループiのデータの同時密度(母集団パラメータをサンプル推定値に置き換え)であるとします。
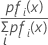
最大事後確率は、ln [pifi(x)]の最大値と等しくなります。
fi(x)が正規分布の場合、次のようになります。
ln [pifi(x)] = -0.5 [di2(x) – 2 ln pi] – (定数)
角カッコで囲まれた項は、xとグループiとの一般化二乗距離と呼ばれ、di2(x)と表されます。ただし、
di2(x) = -2[mi' Sp-1 x - 0.5 mi' Sp-1mi + ln pi] + x' Sp-1x
角カッコで囲まれた項は、線形判別関数です。事前確率なしの場合との違いは、定数項の変更だけです。最大事後確率は最小の一般化距離と等しくなりますが、これが最大の線形判別関数と等しいことに留意してください。
