ステップ1:分数を判断する
変動の比率を使用して、データの期待値からの逸脱度の大部分を占める主成分(主軸とも呼ばれる)の最小の数を判断します。全変動の許容可能な割合を説明する主成分を保持します。許容可能な水準は用途によって変わります。第1成分、第2成分、または第3成分が全変動の大部分を占めるのが理想的です。
必要な主成分の最小値が、分析に入力する成分数と一致しない場合、適切な成分数を使用して分析を繰り返します。
分割表の分析
| 軸 | 変動 | 比率 | 累積 |
|---|---|---|---|
| 1 | 0.0391 | 0.4720 | 0.4720 |
| 2 | 0.0304 | 0.3666 | 0.8385 |
| 3 | 0.0109 | 0.1311 | 0.9697 |
| 4 | 0.0025 | 0.0303 | 1.0000 |
| 合計 | 0.0829 |
主要な結果:軸、比率、累積
これらの結果は、10 x 5分割表の全変動を4つの成分(軸)に分解することを示します。4成分で説明される全変動は0.0829です。全変動の中でも、第1成分は変動の47.2%(比率 = 0.4720)を占め、第2成分は変動の36.66%(比率 = 0.3666)を占めます。これらの2成分で、全変動の83.85%(累積 = 0.8385)を占めます。このため、2つの成分を分析に指定すれば十分かもしれません。
ステップ2:主成分を解釈する
品質の値を使用して、成分によって表される列変動または行変動の比率を判断します。品質の値は常に0~1の範囲にあります。品質の値が大きいほど、行または列は成分によって十分に表現されることを示します。品質の値が低いほど、表現は低下します。行と列の品質の値により、成分は解釈しやすくなります。
行および・または列の寄与度の値を使用して、成分ごとの変動に最も寄与する列と行のカテゴリを評価します。成分を視覚的に解釈するには、行プロットまたは列プロットを使用します。
行寄与度
| 成分1 | 成分2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名前 | 品質 | 質量 | 変動 | 座標 | 相関 | 寄与 | 座標 | 相関 | 寄与 |
| 1 | 地質学 | 0.916 | 0.107 | 0.137 | -0.076 | 0.055 | 0.016 | -0.303 | 0.861 | 0.322 |
| 2 | 生物化学 | 0.881 | 0.036 | 0.119 | -0.180 | 0.119 | 0.030 | 0.455 | 0.762 | 0.248 |
| 3 | 化学 | 0.644 | 0.163 | 0.021 | -0.038 | 0.134 | 0.006 | -0.073 | 0.510 | 0.029 |
| 4 | 動物学 | 0.929 | 0.151 | 0.230 | 0.327 | 0.846 | 0.413 | -0.102 | 0.083 | 0.052 |
| 5 | 物理学 | 0.886 | 0.143 | 0.196 | -0.316 | 0.880 | 0.365 | -0.027 | 0.006 | 0.003 |
| 6 | 工学 | 0.870 | 0.111 | 0.152 | 0.117 | 0.121 | 0.039 | 0.292 | 0.749 | 0.310 |
| 7 | 微生物学 | 0.680 | 0.046 | 0.010 | -0.013 | 0.009 | 0.000 | 0.110 | 0.671 | 0.018 |
| 8 | 植物学 | 0.654 | 0.108 | 0.067 | 0.179 | 0.625 | 0.088 | 0.039 | 0.029 | 0.005 |
| 9 | 統計学 | 0.561 | 0.036 | 0.012 | -0.125 | 0.554 | 0.014 | -0.014 | 0.007 | 0.000 |
| 10 | 数学 | 0.319 | 0.098 | 0.056 | -0.107 | 0.240 | 0.029 | 0.061 | 0.079 | 0.012 |
主要な結果:品質、寄与度、列・列プロット
この分析では、2つの主成分を計算します。行寄与度表では、品質の最大値は、動物学(0.929)と地質学(0.916)で発生します。このため、これら2つの行は2つの成分で最もよく表現されます。最も説明できないフィールドは数学で、品質の値は0.319です。
動物学(0.413)と物理学(0.365)は成分1の変動に最も寄与します。地質学(0.322)、工学(0.310)、生化学(0.248)が成分2の変動に最も寄与します。
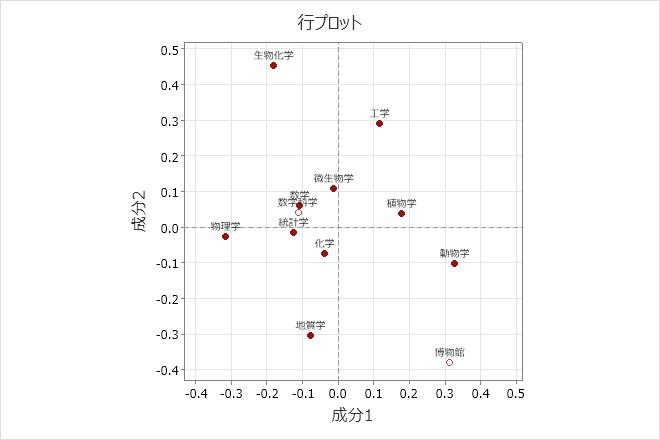
行プロットは主行座標を示します。動物学と物理学を最もよく説明している成分1について見ると、これらの2つのフィールドが原点から一番離れているものの、記号は反対であることがわかります。このため、成分1は動物学および植物学などの生物学と物理学を対比します。成分2は生化学および工学と地質学を対比します。
ステップ3:カテゴリ間の関係を調べる
行カテゴリと列カテゴリの計算された変動値を調べて、起こりうる関係を調べます。関係性が強いカテゴリほど変動値が高く、合計カイ二乗値に最も寄与することを示します。
非対称な行または列プロットを使用して、起こりうる関係性を視覚的に調べることができます。行プロットでは、行プロファイルと列頂点が近いほど、行プロファイルと列カテゴリの相関性が高くなります。列プロットでは、列プロファイルと行頂点が近いほど、列プロファイルと行カテゴリの相関性が高くなります。
行寄与度
| 成分1 | 成分2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名前 | 品質 | 質量 | 変動 | 座標 | 相関 | 寄与 | 座標 | 相関 | 寄与 |
| 1 | 地質学 | 0.916 | 0.107 | 0.137 | -0.076 | 0.055 | 0.016 | -0.303 | 0.861 | 0.322 |
| 2 | 生物化学 | 0.881 | 0.036 | 0.119 | -0.180 | 0.119 | 0.030 | 0.455 | 0.762 | 0.248 |
| 3 | 化学 | 0.644 | 0.163 | 0.021 | -0.038 | 0.134 | 0.006 | -0.073 | 0.510 | 0.029 |
| 4 | 動物学 | 0.929 | 0.151 | 0.230 | 0.327 | 0.846 | 0.413 | -0.102 | 0.083 | 0.052 |
| 5 | 物理学 | 0.886 | 0.143 | 0.196 | -0.316 | 0.880 | 0.365 | -0.027 | 0.006 | 0.003 |
| 6 | 工学 | 0.870 | 0.111 | 0.152 | 0.117 | 0.121 | 0.039 | 0.292 | 0.749 | 0.310 |
| 7 | 微生物学 | 0.680 | 0.046 | 0.010 | -0.013 | 0.009 | 0.000 | 0.110 | 0.671 | 0.018 |
| 8 | 植物学 | 0.654 | 0.108 | 0.067 | 0.179 | 0.625 | 0.088 | 0.039 | 0.029 | 0.005 |
| 9 | 統計学 | 0.561 | 0.036 | 0.012 | -0.125 | 0.554 | 0.014 | -0.014 | 0.007 | 0.000 |
| 10 | 数学 | 0.319 | 0.098 | 0.056 | -0.107 | 0.240 | 0.029 | 0.061 | 0.079 | 0.012 |

主要な結果:変動、非対称行/列プロット
行寄与度表では、Inert(変動)という列は、各行が寄与する全変動の比率です。つまり、地質学の全カイ二乗統計量への寄与度は13.7%です。動物学は変動の最大値(0.230)を持ちます。このため、動物学はカイ二乗値の合計に23%寄与し、列カテゴリ(資金)との関係性が他の行カテゴリよりも強いです。
非対称行プロットでは、行の点は学問分野を表し、列の点は資金水準(Aは最大の資金水準、Dは最小の資金水準、Eは資金なし)を表します。生化学は列カテゴリEに最も近く、学問分野としての生化学が、この研究では資金調達が難しい研究者の割合が最も高いことを示しています。
