行プロット
注
デフォルトでは、全変動の最大量を占める最初の2つの主成分のデータ点が表示されます。他の主成分(軸)をプロットに表示するには、グラフをクリックして、分析実行時に成分数を入力します。
解釈
行プロットを使用して、行カテゴリ間の関係を確認して、行カテゴリに関係のある主成分を解釈しやすくします。原点からかなり離れているデータ点は、影響力が大きいカテゴリを示します。プロットの両端にあるデータ点は、成分がこれらのカテゴリを対比することを示します。
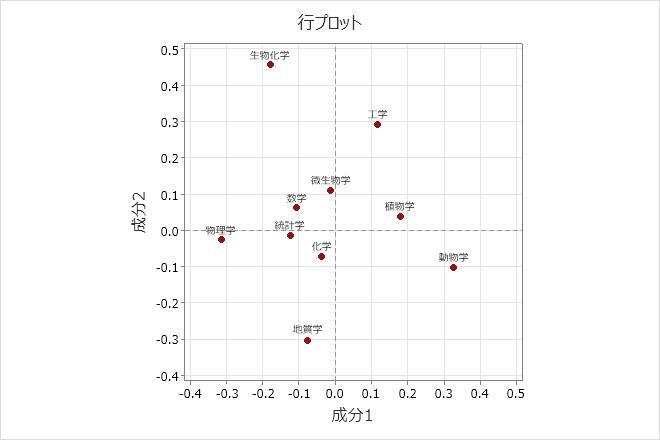
行プロットは、主行座標を示しています。動物学と物理学をもっともよく説明している成分1について見ると、これらの2つのフィールドが原点から一番離れているものの、記号は反対であることがわかります。このため、成分1は動物学や植物学などの生物学と物理学を対比します。成分2は生化学および工学と地質学を対比します。
列プロット
注
デフォルトでは、全変動の最大量を占める、最初の2つの主成分のデータ点を表示します。他の主成分(軸)をプロットに表示するには、グラフをクリックして、分析実行時に成分数を入力します。
解釈
列プロットを使用して、列カテゴリ内の関係を調べて、列カテゴリと関係のある主成分を解釈しやすくします。原点からかなり離れているデータ点は、カテゴリの影響度が大きいことを示します。プロットの両端にあるデータ点は、成分がこれらのカテゴリを対比していることを示します。
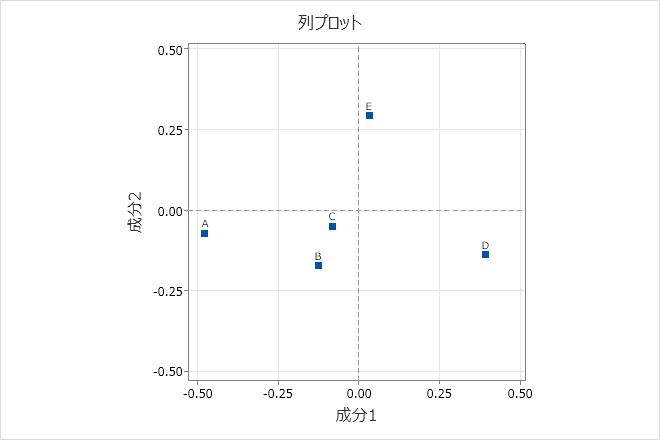
列プロットは、主列座標を示します。成分1は、資金カテゴリAとDを最もよく説明しており、これらの2つのカテゴリが原点から一番離れているものの、記号は反対であることを示しています。したがって、成分1はこれら2つの資金カテゴリを対比しています。成分2は、資金カテゴリEを最もよく説明し、このカテゴリと他の資金カテゴリを対比します。
対称プロット
注
デフォルトでは、最初の2つの主成分のデータ点が表示され、全変動の最大量を占めます。他の主成分(軸)をプロットに表示するには、グラフをクリックして、分析実行時に成分数を入力します。
解釈
重要
対称プロットの行と列の距離では、2つの異なるマッピングを使用します。行と列の距離は標準化されていないので、行カテゴリと列カテゴリの距離は容易には解釈できません。行カテゴリと列カテゴリの距離を解釈するには、非対称プロットを使用します。
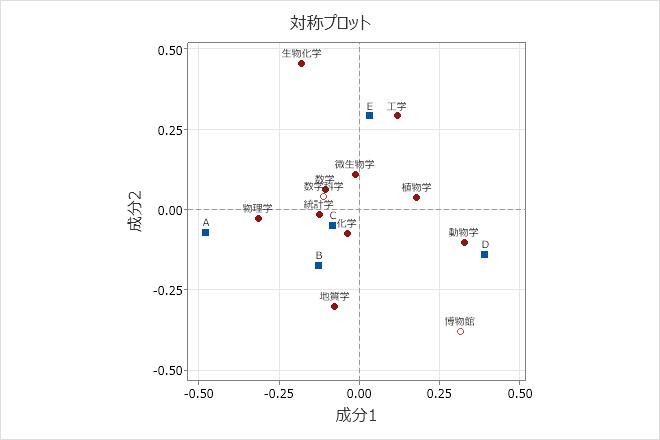
この対称プロットは、主行座標と主列座標を表示します。成分1は動物学と物理学の行カテゴリを最もよく説明しており、これらの2つのフィールドが原点から一番離れているものの、記号は反対です。成分1は、列カテゴリAと列カテゴリDを対比します。成分2は、生化学および工学の行カテゴリと地質学および博物館を対比し、列カテゴリEを最もよく説明します。
非対称行プロット
注
デフォルトでは、全変動の最大量を占める最初の2つの主成分のデータ点が表示されます。他の主成分(軸)をプロットに表示するには、グラフをクリックして、分析実行時に成分数を入力します。
解釈
非対称行プロットを使用して、行と列カテゴリの関係を確認して、行カテゴリに関係のある主成分を解釈しやすくします。原点からかなり離れているデータ点は、影響力が大きいカテゴリを示します。プロットの両端にあるデータ点は、成分がこれらのカテゴリを対比することを示します。行カテゴリのデータ点が列カテゴリのデータ点に近くなるほど、列カテゴリの行プロファイルの値は高くなります。
注
非対称プロットにより、行項目点間距離と列項目点間距離を直観的に解釈でき、2つの成分が全変動の大部分を占めているときに特に当てはまります。ただし、非対称プロットのデータ点は、グラフの中心付近で互いに近すぎるように見え、結果を表示するのが難しくなることがあります。このケースでは、行または列のカテゴリの関係をよりはっきり表示するために、対称プロットも表示したいと思うかもしれません。

この非対称な行プロットでは、行のデータ点は学問分野を表し、列のデータ点は資金水準(Aは資金の最大水準、Dは最小水準です。Eは資金なしです)を表します。
資金クラスのうち、成分1は資金のレベルを対照し、成分2は資金があるか(AからD)ないか(E)を対照します。学問分野の中で、「物理学」が資金を一番多く受け、「動物学」が一番少なく受ける傾向にあります。生化学には資金調達が難しい傾向がありますが、資金調達された場合、最小カテゴリの資金(D)に属することは滅多にありません。学問分野の中では、生化学が列カテゴリEに最も近く、1つの学問分野としての生化学では、こうした研究に携わる資金調達が難しい研究者の割合が最も高いです。博物館は資金調達しやすい傾向がありますが、学問分野の研究者よりも水準は低いです。ただし、グラフの中心にあるデータ点のクラスターにより、結果を表示するのは難しくなります。学問分野に関係する成分を解釈しやすくするには、非対称列プロットまたは対称行プロットも調べます。
非対称列プロット
注
デフォルトでは、全変動の最大量を占める最初の2つの主成分のデータ点を表示します。他の主成分(軸)をプロットに表示するには、グラフをクリックして、分析実行時に成分数を入力します。
解釈
非対称列プロットを使用して、行と列カテゴリ間の関係を確認して、主成分を解釈しやすくします。原点からかなり離れているデータ点は、影響力が大きいカテゴリを示します。プロットの両端にあるデータ点は、成分がこれらのカテゴリを対比することを示します。列カテゴリのデータ点が行カテゴリのデータ点に近いほど、行カテゴリに対する列プロファイルの値が高くなります。
注
非対称プロットにより、行項目点間距離と列項目点間距離を直観的に解釈でき、2つの成分が全変動の大きな比率を表す場合は特に当てはまります。ただし、非対称プロットのデータ点は、グラフの中心で互いの位置が近すぎ、結果を表示するのが難しくなることがあります。こうしたケースでは、対称プロットを表示して、行カテゴリ間または列カテゴリ間の関係をよりはっきり表示させたくなることもあります。
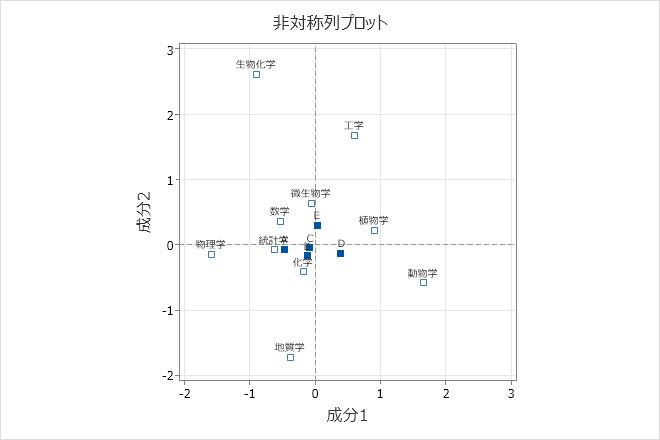
この対称列プロットでは、行の点は学問分野を表し、列の点は資金水準を表します(Aの資金水準は最大で、Dは最小です。Eは資金なしです)。
学問分野の中では、成分1は、物理学と動物学を対比し、成分2は生化学と地質学を対比します。資金クラスのうち、成分1は資金のレベルを対照し、成分2は資金があるか(AからD)ないか(E)を対比します。物理学の資金水準は最大で、動物学が最小になる傾向にあります。プロットの中心に近い学部は、資金プロファイルが全体の資金プロファイルに類似する傾向があります。資金カテゴリEが行カテゴリ「微生物学」に最も近く、資金カテゴリEの微生物学の研究者の割合が最大であることを示しています。
