主成分分析の方法と計算式

主成分分析では、Minitabは、変数の相関行列または共分散行列の直交固有ベクトルをまず見つけます。主成分の行列は、固有ベクトル行列と独立変数の行列の積です。第1主成分では、データ全体のばらつきが大きな割合を占めます。第2主成分では、データの全体のばらつきが二番目に大きな割合を占めます。主成分の目的は、最少数の成分で最大の分散を説明することです。

主成分の係数は、固有値がそれぞれ異なり0でない場合には、一意です（符号の違いは除きます）。固有値が繰り返される場合は、同じ固有値に対応するすべての主成分ベクトルによって「表される空間」は一意ですが、個々のベクトルは一意ではありません。つまり、固有値（成分の分散）が常に同じであったとしても、Minitabが出力時に表示する係数と本または別のプログラムの係数は一致しません。

共分散行列の順位がr < pの場合（pは変数の数）、p - r固有値は0に等しくなります。これらの固有値に対応する固有ベクトルは、一意でない場合もあります。この現象は、測定値の数がpよりも少ない場合、または多重共線性がある場合に発生することがあります。

各変数に対応する係数で構成される固有ベクトルは、主成分スコアの計算で使用される変数ごとの重みです。固有ベクトルは、共分散行列Sまたは相関行列Rのスペクトル分解における直交行列の列として取得します。より具体的には、Rが対称的なので、直交行列VがV'RV = D、すなわちR = VDV'（Dは、対角要素が固有値直交行列）といった形で存在します。固有値はVの列です。固有値はR = VDV'から求められます。

表記

計算式

スコアは、データの分散を説明する元の変数の線形結合です。

スコアは次のように計算されます: Z = YV

表記

計算式

固有値は、共分散行列または相関行列（「固有ベクトル」のトピックを参照）のスペクトル分解における対角行列の対角要素です。固有値は、主成分Z = V Yのサンプル分散でもあります。

表記

計算式

k番目の主成分によって説明されるサンプルのばらつきの累積比率は、次のように計算されます。

表記

用語	説明
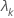	k番目の固有値
p	変数の数

計算式

表記

用語	説明
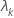	k番目の固有値
p	変数の数

計算式

マハラノビス距離は、データの共分散構造を利用して、多変量空間の各データ点と全体平均（重心）との距離を測定します。

Minitabは、外れ値プロットの参照線を表示して、マハラノビス距離の値が大きい外れ値を特定します。参照線は、次の計算式で定義します。

n – p – 1 が0の場合、Minitabは、参照線なしで外れ値プロットを表示します。

表記

用語	説明
Yi	i行目のデータ値ベクトル
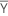	平均ベクトル
S-1	共分散行列の逆行列
p	変数の数
n	非欠損データ行の数