ステップ1:主成分数を判断する
- 主成分を説明する分散の比率
- 累積比率を使用して、主成分が説明する分散の総量を判断します。許容可能な水準の分散を説明する主成分を保持します。許容可能な水準は用途によって変わります。記述目的であれば、説明される分散が80%は必要です。しかし、データを別の方法で分析する場合は、主成分によって説明される分散が少なくとも90%は必要になります。
- 固有値
- 固有値のサイズを使用して主成分の数を決定できます。固有値が最大の主成分を保持します。たとえば、カイザー基準を使用して、1より大きな固有値を持つ主成分のみを使用します。
- 固有値(Scree)プロット
- 固有値プロットは、固有値を最大から最小に順序付けします。理想的なパターンは急な曲線で、それに折れ線、直線が続きます。線の傾向が始まる始点の前に急な曲線の成分を使用します。
相関行列の固有分析
| 固有値 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累積 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
固有ベクトル
| 変数 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 収入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 学歴 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年齢 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 居住年数 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 勤続年数 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 貯蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 借金 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| クレジットカード数 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
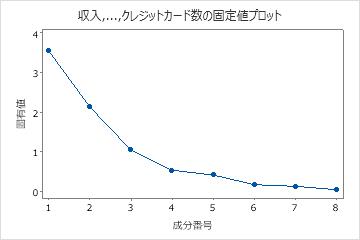
主要な結果:累積、固有値、固有値プロット
これらの結果では、最初の3つの主成分の固有値が1よりも大きくなります。3つの主成分はデータ内の分散の84.1%を説明します。固有値プロットは、固有値が直線になるのは、3つの主要成分の後であることを示しています。84.1%がデータで説明されている十分な量の変動である場合、最初の3つの主成分を使用する必要があります。
ステップ2:元の変数の観点から各主成分を解釈する
各主成分を解釈するには、元の変数の大きさと方向を調べます。係数の雑多位置が大きいほど、成分の計算において対応する変数の重要性が高まります。重要とみなされるように係数の絶対値がどれくらい大きくあるべきなのかは、主観的な話です。特定の知識を使用して、相関値がどの水準で重要であるかを判断します。
相関行列の固有分析
| 固有値 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累積 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
固有ベクトル
| 変数 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 収入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 学歴 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年齢 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 居住年数 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 勤続年数 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 貯蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 借金 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| クレジットカード数 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
主要な結果:PC、負荷量プロット
これらの結果では、最初の主成分に年齢、居住地、雇用、貯蓄との大きな正の関係があるため、この成分は主に長期的な財政安定性を測ります。第2の成分には、債務およびクレジットカードとの大きな負の関係があるため、この成分は主に申請者のクレジット履歴を測ります。第3の成分には、所得、教育、クレジットカードとの大きな負の関係があるため、この成分は主に申請者の学歴と所得の資格を測ります。
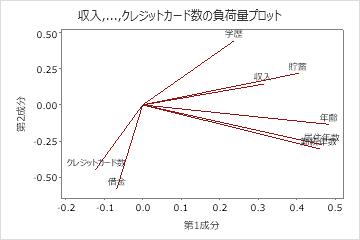
負荷量プロットには、最初の2つの成分の結果が視覚的に表示されます。年齢、居住地、雇用、貯蓄は成分1にとって大きな正の負荷となっているため、この成分は長期的な財務安定性を測ります。債務およびクレジットカードは、成分2にとって大きな負の負荷となっているため、この成分は主に申請者のクレジット履歴を測ります。
ステップ3:外れ値を特定する
外れ値プロットを使用して、データの外れ値を特定します。参照ラインの上にある点は外れ値です。外れ値は分析の結果に大きな影響を与えることがあります。したがって、データに外れ値があった場合、観測値を調べて異常な理由を理解する必要があります。測定値やデータ入力の誤差を修正してください。特定の原因に関連するデータを削除し、分析を再度実行することを検討してください。
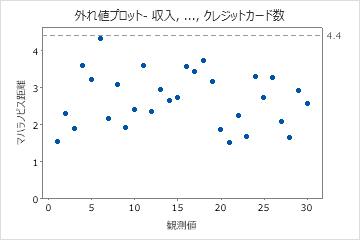
主要な結果:外れ値プロット
これらの結果に外れ値はありません。すべてのデータ点は、参照線よりも下側にあります。
ヒント
ポインタを外れ値プロットの任意の点に当て、観測値を識別します。を使用して、プロットの複数の外れ値をブラシ掛けし、ワークシートの観測値にフラグを立てます。
