固有値
固有値(特性値や最近値とも呼ばれます)は、主要成分の分散です。
解釈
固有値のサイズを使用して主成分の数を決定できます。固有値が最大の主成分を保持します。たとえば、カイザー基準を使用して、1より大きな固有値を持つ主要成分のみを使用します。
固有値のサイズを視覚的に比較するには、固有値プロットを使用します。固有値プロットにより、固有値のサイズを元に成分の数を決定できます。
相関行列の固有分析
| 固有値 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累積 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
固有ベクトル
| 変数 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 収入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 学歴 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年齢 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 居住年数 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 勤続年数 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 貯蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 借金 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| クレジットカード数 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
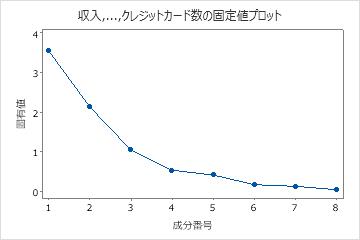
これらの結果では、最初の3つの主要成分の固有値が1よりも大きくなります。3つの主要成分はデータ内の分散の84.1%を説明します。固有値プロットは、固有値が直線になるのは、3つの主要成分の後であることを示しています。もし84.1%がデータで説明される適切な変動量である場合、最初の3つの主要成分を使ってください。
比率
「比率」は、各主成分が説明するばらつきの比率です。
解釈
比率を使用して、どの主成分がデータのばらつきの大部分を説明するかを判断します。比率が高いほど、主成分が説明するばらつきが大きくなります。比率のサイズは、主成分を保持するのに十分なほど重要かを判断しやすくします。
たとえば、0.621の比率を持つ主成分は、データのばらつきの62.1%を説明します。したがって、この成分を含めることは重要です。別な成分の比率は0.005であり、データのばらつきの0.5%しか説明しません。この成分は、含めるほど重要とは言えません。
累積
累積は、連続主成分によって説明されるサンプルのばらつきの累積比率です。
解釈
累積比率を使用して、連続主成分が説明する分散の総量を評価します。累積比率により、使用する主成分の数を決定しやすくなります。許容可能な水準の分散を説明する主成分を保持します。許容可能な水準は用途によって変わります。
たとえば、記述目的だけで主成分を使用する場合、主成分によって説明される分散の80%しか必要ありません。しかし、データを別の方法で分析する場合は、主成分によって説明される分散が少なくとも90%は必要になります。
主成分(PC)
注
相関行列を使用する場合、正しい成分スコアを得るには、変数を標準化する必要があります。
解釈
各主成分を解釈するには、元の変数の係数の大きさと向きを調べます。係数の絶対値が大きくなるほど、成分を計算するうえで対応する変数が重要になります。係数が重要だとみなされるために係数の絶対値がどの程度大きくならなければいけないかという点は主観的です。専門知識を使用して、相関値が重要になる水準を決定します。
相関行列の固有分析
| 固有値 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累積 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
固有ベクトル
| 変数 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 収入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 学歴 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年齢 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 居住年数 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 勤続年数 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 貯蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 借金 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| クレジットカード数 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
これらの結果では、最初の主成分は、年齢、居住年数、勤続年数、貯蓄と大きな正の関係があります。この成分を、申請者の長期的な財務安定性の主な測度として解釈できます。2番目の成分は、借金、クレジットカードと大きな負の関係があるので、この成分は、申請者のクレジット履歴を主に測定します。3番目の成分は、収入、教育、クレジットカードと大きな負の関係があるので、この成分は、申請者の学業面および収入面の資格を主に測定します。
スコア
スコアは、主成分ごとの係数で決定したデータの線形結合です。観測値のスコアを取得するには、主成分の代わりに一次方程式の値を使用します。相関行列を使用する場合、一次方程式を使用するときに正しい成分スコアを得るには、変数を標準化する必要があります。
注
観測値ごとに計算されたスコアを取得するには、保存をクリックして列を入力し、分析実行時にワークシートのスコアを保存します。グラフ上の1番目と2番目の成分のスコアを視覚的に表示するには、グラフをクリックして、分析実行時にスコアプロットを選択します。
相関行列の固有分析
| 固有値 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 比率 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 累積 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
固有ベクトル
| 変数 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 収入 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 学歴 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 年齢 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 居住年数 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 勤続年数 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 貯蓄 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 借金 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| クレジットカード数 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
これらの結果では、最初の主成分のスコアは、PC1の下にリスト表示される係数を使用して、標準化データを基に計算できます。
PC1 = 0.314(収入)+0.237(学歴)+0.484(年齢)+0.466(居住年数)+0.459(勤続年数)+0.404(貯蓄)ー0.067(借金)ー0.123(クレジットカード数)
距離
マハラノビス距離とは、データ点と多変量空間の重心(全体平均)との距離のことです。
注
各観測値の距離を計算するには、分析を実行するときに保存をクリックし、ワークシートに列を入力して距離を保存します。グラフに距離を表示するには、分析を実行するときにグラフをクリックして、外れ値プロットを選択する必要があります。
解釈
マハラノビス距離を使用して外れ値を特定します。マハラノビス距離を調査することは、距離においてそれぞれの変数の尺度と変数間の相関をまとめて処理するため、変数を1つずつ確認していく方法に比べて、より強力に外れ値を検出できる多変量手法です。
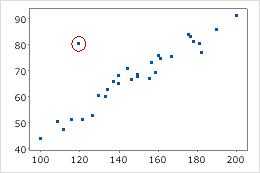
たとえば、変数を1つ1つ検討していくと、丸の付いたデータ点のx値もy値も、異常になることはありません。ただし、このデータ点は、2つの変数の相関構造に一致しません。したがって、このデータ点のマハラノビス距離は、異常に大きくなります。
観測値が外れ値とみなされるほど距離値が大きいかどうかを評価するには、外れ値プロットを使用します。
固有値(Scree)プロット
固有値(Scree)プロットは主要成分の数とそれに対応する固有値を表示します。固有値(Scree)プロットは固有値を最大値から最小値に並べます。相関行列の固有値は主要成分の分散と等しくなります。
固有値(Scree)プロットを表示するには、グラフをクリックして、分析を実行するときに固有値プロットを選択します。
解釈

この固有値(Scree)プロットは、固有値が直線になるのは、3つの主要成分の後であることを示しています。このため、残りの主要成分は変動性の非常に小さな比率を占めており(0に近い)、おそらく重要ではありません。
スコアプロット
スコアプロットは、第1主成分分析のスコアと第2主成分分析のスコアとの関係をグラフにします。
スコアプロットを表示するには、グラフをクリックして、分析を実行するときにスコアプロットを選択する必要があります。
解釈
最初の2つの成分が、データのほとんどの分散を説明する場合は、スコアプロットを使用してデータ構造を評価し、クラスター、外れ値、傾向を検出できます。このプロットのデータをグループ化する場合、データ内に2つ以上の異なる分布があることを示すことがあります。データが正規分布に従い、外れ値が存在しなければ、点はゼロ付近にランダムに分布します。

このスコアプロットでは、下隅にあるデータ点が外れ値の可能性があります。この点を調査する必要があります。
ヒント
観測値ごとに計算されたスコアを確認するには、ポインタをグラフのデータ点の上に置きます。 他の成分のスコアプロットを作成するには、スコアを保存し、を使用します。
負荷量プロット
負荷量プロットは、第1成分の各変数の係数と第2成分の係数との関係をグラフにします。係数は、各主成分の固有ベクトルを構成する値です。係数は、成分の各変数の相対的な重みを示します。
負荷量プロットを表示するには、グラフをクリックして、分析を実行するときに負荷量プロットを選択します。
解釈
負荷量プロットを使用して、どの変数が各成分に最大の効果があるかを特定します。係数の範囲は -1 から 1 です。-1 または 1 に近い係数は、変数が成分に強く影響することを示します。係数が 0 に近い場合は、変数が成分に及ぼす影響が弱いことを示します。係数を評価することは、変数の観点から各成分を特徴付けるのにも役立ちます。
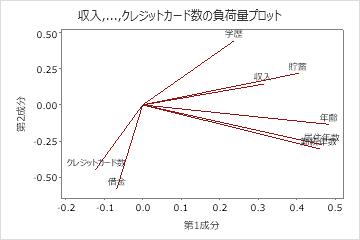
この負荷量プロットでは、年齢、居住年数、勤続年数、貯蓄には、成分1に大きな正の負荷量があるので、この成分は、申請者の長期的な財務安定性を主に測定します。借入金とクレジットカードは、成分2に大きな負の係数があるため、この成分は主に申請者の信用履歴を測定します。
バイプロット
バイプロットは、スコアプロットと負荷量プロットを重ね合わせて表示します。
バイプロットを表示するには、グラフをクリックして、分析を実行するときにバイプロットを選択します。
解釈
1つのグラフの最初の2つの成分のデータ構造と負荷量を評価するには、バイプロットを使用します。Minitabは、両方の成分の負荷量と同様に、第2主成分のスコアと第1主成分のスコアとの関係をグラフにします。
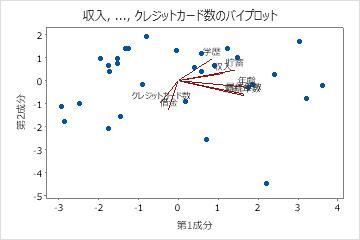
- 年齢、居住年数、勤続年数、貯蓄には、成分1に大きな正の負荷量があります。このため、この成分は、申請者の長期的な財務安定性に焦点を当てます。
- 借金とクレジットカード数は、成分2に大きな負の負荷量を持ちます。したがって、この成分は申請者のクレジット履歴に焦点を当てます。
- 右下隅のデータ点が外れ値である可能性があります。この点を調査する必要があります。
外れ値プロット
外れ値プロットは、観測値ごとのマハラノビス距離と外れ値を特定する参照線を示します。マハラノビス距離とは、各データ点と多変量空間の重心(全体平均)との距離のことです。マハラノビス距離を調査することは、それぞれの変数の尺度と変数間の相関をまとめて処理するため、変数を1つずつ確認していく方法に比べて、より強力に外れ値を検出できます。
外れ値プロットを表示するには、グラフをクリックして、分析を実行するときに外れ値プロットを選択する必要があります。
解釈
外れ値プロットを使用して、データの外れ値を特定します。参照ラインの上にある点は外れ値です。
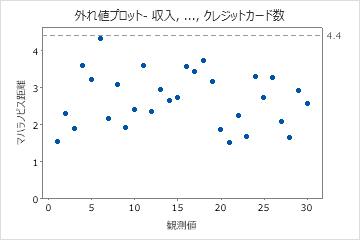
これらの結果に外れ値はありません。すべてのデータ点は、参照線よりも下側にあります。
ヒント
ポインタを外れ値プロット上の適当な点の上に置くと、観測値を特定することができます。プロット上の複数の外れ値をブラッシングしてワークシートの観測値にフラグを立てるにはを使用します。
