多重コレスポンデンス分析の列寄与度

列プロファイルは、d次元の空間にあります。主軸の完全なセットはこの空間を対象としています。g_j1, g_j2, g_j3, ..., g_jdは、主軸の観点では、列プロファイルjの座標と考えられます。これらの座標は主列座標と呼ばれます。列プロファイルjのk番目の主座標はg_jkです。

最適なk次元部分空間は、最初のk主軸の対象になります。最適なk次元部分空間に列プロファイルjを投影する場合、g_j1, ..., g_jkは、この部分空間のプロファイルの主列座標です。

列プロファイルiと主成分kの相関は次のように計算します。

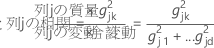
Minitabでは、列ごとの相対的変動を計算します。絶対的変動は相対的変動と全変動の積です。

すべての主成分の列jの相関の和は1です。最初のk主座標の和は、列プロファイルjと最適なk次元部分空間と関係のある品質です。

表記

セル内の変動は次のように計算します。

すべてのセル変動の和が、その表の全変動（単に「変動」と呼ぶこともあります）です。

セルの相対変動は次のように計算します。

列プロファイルは、c次元の空間にあります。低い次元の部分空間は、主軸（主成分とも呼ばれる）の対象となります。第1成分軸は、全変動の最大量を占めるc次元空間のベクトルとして選択されています。このため、第1主軸は、最適な（つまり、適切な基準を使用してプロファイルに最も近い）1次元部分空間を対象とします。第2主軸は、残りの変動の最大量を占めるc次元空間のベクトルとして選択されています。このため、最初の2つの主軸は、最適な2次元部分空間を対象とします。3番目の主軸は、最初の2つの主軸が占める変動の次に、残りの変動の最大量を占めるc次元空間のベクトルとして選択されています。このため、最初の3つの主軸は、最適な3次元部分空間を対象とします。

d = （r − 1）か（c − 1）のいずれか小さい方だとします。列プロファイルは実際には、完全なc次元空間（つまり、完全なr次元空間）のd次元部分空間にあります。したがって、主軸の数は多くてもdまでです。

列プロファイルjと最適なk次元部分空間と関係のある品質は次のように計算します。

品質は必ず0～1の範囲の値であり、値が大きいほど近似が良好であることを示します。

表記

それぞれの列は軸ごとの変動に寄与します。軸kに対する列jの寄与度は、軸kの変動率として、次のように計算します。

すべての列jにわたる主軸kの寄与度の和は1です。

表記

列jの質量は次のように計算します。

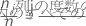
c列目の質量のベクトルは平均列プロファイルと同じです。

成分kの標準化された列座標は、成分kの主座標をk番目の変動の平方根で割った値です。