ステップ1:分数を判断する
変動の比率を使用して、データの期待値から得られる偏差の大部分を占める主成分(主軸とも呼ばれる)の最小値を決定します。全変動の許容可能な比率を説明する主成分を保持します。許容可能な水準は用途によって変わります。第1成分、第2成分、または第3成分が全変動の大部分を占めるのが理想的です。
必要な主成分の最小値が、分析に入力する成分数と一致しない場合、適切な成分数を使用して分析を繰り返します。
指標行列の分析
| 軸 | 変動 | 比率 | 累積 | ヒストグラム |
|---|---|---|---|---|
| 1 | 0.4032 | 0.4032 | 0.4032 | ****************************** |
| 2 | 0.2520 | 0.2520 | 0.6552 | ****************** |
| 3 | 0.1899 | 0.1899 | 0.8451 | ************** |
| 4 | 0.1549 | 0.1549 | 1.0000 | *********** |
| 合計 | 1.0000 |
主要な結果:軸、比率、累積比率
これらの結果は、全変動を4つの成分に分解したものを示します。4成分が説明される全変動は1.000です。全変動のうち、第1成分(軸)は変動の40.32%、第2成分は25.20%を占めます。これら2つの成分で、全変動の65.52%を占めます。このため、分析で2つの成分を指定しても不十分なことがあります。第3成分を追加することで、変動の累積比率は84.51%に上昇します。
ステップ2:主成分を解釈する
品質の値を使用して、カテゴリごとの成分によって表される変動の比率を判断します。品質の値は常に0~1の範囲にあります。品質の値が大きいほど、行または列は成分によって十分に表現されます。品質の値が小さいほど、十分に表現されないことを示します。品質の値により、成分は解釈しやすくなります。
列の寄与度の値を使用して、各成分の変動に最も寄与するカテゴリを評価します。成分を視覚的に解釈するには、列プロットを使用します。
指標行列の分析
| 軸 | 変動 | 比率 | 累積 | ヒストグラム |
|---|---|---|---|---|
| 1 | 0.4032 | 0.4032 | 0.4032 | ****************************** |
| 2 | 0.2520 | 0.2520 | 0.6552 | ****************** |
| 3 | 0.1899 | 0.1899 | 0.8451 | ************** |
| 4 | 0.1549 | 0.1549 | 1.0000 | *********** |
| 合計 | 1.0000 |
列寄与度
| 成分1 | 成分2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名前 | 品質 | 質量 | 変動 | 座標 | 相関 | 寄与 | 座標 | 相関 | 寄与 |
| 1 | 小さい | 0.9655 | 0.0424 | 0.2076 | 0.3814 | 0.0297 | 0.0153 | -2.1394 | 0.9357 | 0.7707 |
| 2 | 基準 | 0.9655 | 0.2076 | 0.0424 | -0.0780 | 0.0297 | 0.0031 | 0.4374 | 0.9357 | 0.1576 |
| 3 | 車外放出なし | 0.4739 | 0.2134 | 0.0366 | -0.2844 | 0.4717 | 0.0428 | -0.0197 | 0.0023 | 0.0003 |
| 4 | 車外放出あり | 0.4739 | 0.0366 | 0.2134 | 1.6587 | 0.4717 | 0.2497 | 0.1151 | 0.0023 | 0.0019 |
| 5 | 衝突 | 0.6133 | 0.1926 | 0.0574 | -0.4264 | 0.6095 | 0.0868 | 0.0338 | 0.0038 | 0.0009 |
| 6 | 転倒 | 0.6133 | 0.0574 | 0.1926 | 1.4294 | 0.6095 | 0.2911 | -0.1133 | 0.0038 | 0.0029 |
| 7 | 軽度 | 0.5680 | 0.1353 | 0.1147 | -0.6523 | 0.5018 | 0.1428 | -0.2371 | 0.0663 | 0.0302 |
| 8 | 重度 | 0.5680 | 0.1147 | 0.1353 | 0.7692 | 0.5018 | 0.1684 | 0.2795 | 0.0663 | 0.0356 |
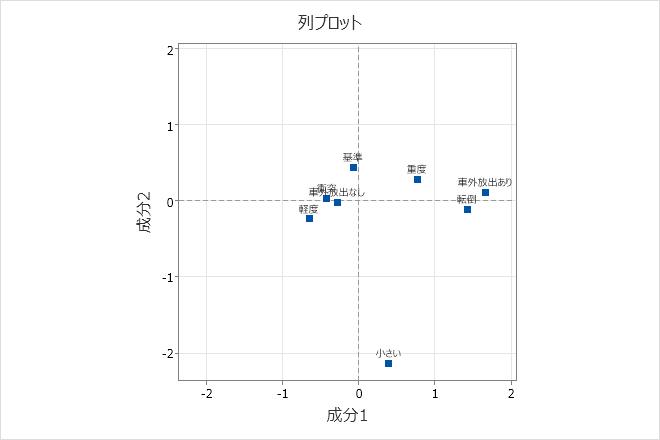
主要な結果:品質、寄与度、列プロット
この分析では、自動車事故に関連するデータに対して2つの主成分を計算します。「列の寄与度」表では、品質の最大値は、車のサイズが「小さい」場合(0.965)と「標準」の場合(0.965)に発生しています。したがって、この2つのカテゴリを最も表しているのは、2つの成分です。事故の重度が最も表現されず、品質の値は「重度」でも「軽度」でも0.568です。「転倒」(0.291)と「車外放出あり」(0.250)が成分1の変動に最も寄与しています。車のサイズが「小さい」(0.771)と「標準」(0.158)は、成分2の変動に最も寄与しています。ただし、2つの成分はこれらのデータのばらつきを十分には説明できないので、これらの結果は注意して解釈する必要があります。
列プロットは主列座標を示します。「転倒」と「車外放出あり」が水平軸の原点からかなり離れているので、成分1は、これら2つのカテゴリを最もよく説明します。重度と軽度は水平軸の原点の反対側にあります。このため、成分1ではこれらのカテゴリの値を対比します。これは、成分1のこうしたカテゴリで相対的に高い寄与度に当てはまります。成分2では、「小さい」という車のサイズを最もよく説明し、「小さい」とその他のカテゴリを対比します。
ステップ3:カテゴリの変動を調べる
列カテゴリの計算された変動値を調べます。カテゴリが期待値から大きく離れるほど、変動値は大きくなり、カイ二乗値全体への寄与度も大きくなります。
列寄与度
| 成分1 | 成分2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | 名前 | 品質 | 質量 | 変動 | 座標 | 相関 | 寄与 | 座標 | 相関 | 寄与 |
| 1 | 小さい | 0.9655 | 0.0424 | 0.2076 | 0.3814 | 0.0297 | 0.0153 | -2.1394 | 0.9357 | 0.7707 |
| 2 | 基準 | 0.9655 | 0.2076 | 0.0424 | -0.0780 | 0.0297 | 0.0031 | 0.4374 | 0.9357 | 0.1576 |
| 3 | 車外放出なし | 0.4739 | 0.2134 | 0.0366 | -0.2844 | 0.4717 | 0.0428 | -0.0197 | 0.0023 | 0.0003 |
| 4 | 車外放出あり | 0.4739 | 0.0366 | 0.2134 | 1.6587 | 0.4717 | 0.2497 | 0.1151 | 0.0023 | 0.0019 |
| 5 | 衝突 | 0.6133 | 0.1926 | 0.0574 | -0.4264 | 0.6095 | 0.0868 | 0.0338 | 0.0038 | 0.0009 |
| 6 | 転倒 | 0.6133 | 0.0574 | 0.1926 | 1.4294 | 0.6095 | 0.2911 | -0.1133 | 0.0038 | 0.0029 |
| 7 | 軽度 | 0.5680 | 0.1353 | 0.1147 | -0.6523 | 0.5018 | 0.1428 | -0.2371 | 0.0663 | 0.0302 |
| 8 | 重度 | 0.5680 | 0.1147 | 0.1353 | 0.7692 | 0.5018 | 0.1684 | 0.2795 | 0.0663 | 0.0356 |
主要な結果:列変動
列寄与度表では、変動(Inert)という列は、各カテゴリが寄与する全変動の比率です。したがって、車外放出ありは、期待値から最も離れており、カイ二乗統計量全体に21.3%寄与します。
