ステップ1:因子数を決定する
- 分散%
- 分散(分散%)の割合を使用して、因子が説明する分散量を決定します。許容可能な水準の分散を説明する因子を保持します。許容可能な水準は用途によって変わります。記述目的であれば、説明される分散が80%しか必要ありません。ただし、データを別の方法で分析する場合は、因子によって説明される分散が少なくとも90%は必要です。
- 分散(固有値)
- 主成分分析を使用して因子を抽出する場合、分散は固有値と一致します。固有値のサイズを使用して因子の数を決定できます。固有値が最大の因子を保持します。たとえば、カイザー基準を使用して、1より大きな固有値を持つ主成分のみを使用します。
- 固有値(Scree)プロット
- 固有値(Scree)プロットは、固有値を最大値から降順に並べます。理想的なパターンは、勾配曲線の後に、曲がり、そして直線が続く形です。直線傾向が始まる最初の点より前の勾配曲線の中に、これらの成分を使用します。
無回転の因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 因子5 | 因子6 | 因子7 | 因子8 | 因子9 | 因子10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 学歴 | 0.726 | 0.336 | -0.326 | 0.104 | -0.354 | -0.099 | 0.233 | 0.147 | 0.097 | -0.142 |
| 容姿 | 0.719 | -0.271 | -0.163 | -0.400 | -0.148 | -0.362 | -0.195 | -0.151 | 0.082 | 0.016 |
| コミュニケーション能力 | 0.712 | -0.446 | 0.255 | 0.229 | -0.319 | 0.119 | 0.032 | 0.088 | 0.023 | 0.204 |
| 会社への適合性 | 0.802 | -0.060 | 0.048 | 0.428 | 0.306 | -0.137 | -0.067 | 0.105 | -0.019 | -0.067 |
| 経歴 | 0.644 | 0.605 | -0.182 | -0.037 | -0.092 | 0.317 | -0.209 | -0.102 | 0.121 | 0.039 |
| 仕事への適合性 | 0.813 | 0.078 | -0.029 | 0.365 | 0.368 | -0.067 | -0.025 | -0.032 | 0.146 | 0.066 |
| 関心表明書 | 0.625 | 0.327 | 0.654 | -0.134 | 0.031 | 0.025 | 0.017 | -0.113 | -0.079 | -0.130 |
| 好感度 | 0.739 | -0.295 | -0.117 | -0.346 | 0.249 | 0.140 | 0.353 | -0.142 | 0.051 | 0.022 |
| 協調性 | 0.706 | -0.540 | 0.140 | 0.247 | -0.217 | 0.136 | -0.080 | -0.105 | -0.020 | -0.162 |
| 将来性 | 0.814 | 0.290 | -0.326 | 0.167 | -0.068 | -0.073 | 0.048 | -0.112 | -0.290 | 0.100 |
| 履歴書 | 0.709 | 0.298 | 0.465 | -0.343 | -0.022 | -0.107 | 0.024 | 0.170 | 0.008 | 0.090 |
| 自信 | 0.719 | -0.262 | -0.294 | -0.409 | 0.175 | 0.179 | -0.159 | 0.230 | -0.098 | -0.061 |
| 分散 | 6.3876 | 1.4885 | 1.1045 | 1.0516 | 0.6325 | 0.3670 | 0.3016 | 0.2129 | 0.1557 | 0.1379 |
| % 分散 | 0.532 | 0.124 | 0.092 | 0.088 | 0.053 | 0.031 | 0.025 | 0.018 | 0.013 | 0.011 |
| 変数 | 因子11 | 因子12 | 共通性 |
|---|---|---|---|
| 学歴 | -0.026 | -0.031 | 1.000 |
| 容姿 | 0.020 | -0.038 | 1.000 |
| コミュニケーション能力 | 0.012 | -0.100 | 1.000 |
| 会社への適合性 | 0.188 | -0.021 | 1.000 |
| 経歴 | 0.077 | 0.009 | 1.000 |
| 仕事への適合性 | -0.176 | 0.008 | 1.000 |
| 関心表明書 | -0.043 | -0.127 | 1.000 |
| 好感度 | 0.064 | 0.012 | 1.000 |
| 協調性 | -0.032 | 0.136 | 1.000 |
| 将来性 | -0.023 | 0.028 | 1.000 |
| 履歴書 | 0.010 | 0.156 | 1.000 |
| 自信 | -0.065 | -0.047 | 1.000 |
| 分散 | 0.0851 | 0.0750 | 12.0000 |
| % 分散 | 0.007 | 0.006 | 1.000 |
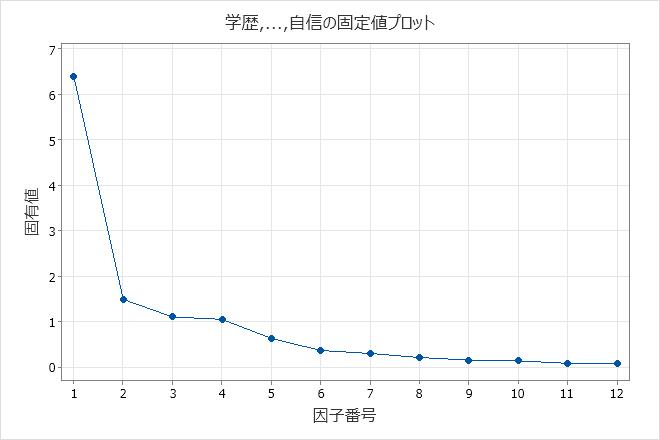
主要な結果:分散%、分散(固有値)、固有値プロット
これらの結果は、主成分抽出法を使用して、すべての因子の無回転因子負荷量を示します。最初の4因子には、1よりも大きい分散(固有値)があります。固有値は、7個以上の因子が使用された場合、あまり大きくは変化しません。したがって、4~6個の因子は、データのばらつきの大半を説明できるように見えます。因子1によって説明されるデータのばらつきの割合は、0.532(53.2%)です。因子4によって説明されるばらつきの割合は、0.088(8.8%)です。固有値(Scree)プロットは、最初の4因子がデータのばらつき全体の大部分を占めることを示しています。その他の因子は変動性についてごく一部しか説明しておらず、重要ではないと考えられます。
ステップ2:因子を解釈する
因子数(ステップ1)を決定後、最尤法を使用して分析を反復できます。負荷量パターンを調べ、各変数に対する影響が最も大きい因子を判断します。-1または1に近い負荷量は、因子が変数に強く影響していることを示します。ゼロに近い負荷量は、変数に対する因子の影響が弱いことを示します。変数によっては、複数の因子に高い負荷を与える場合もあります。
無回転の因子負荷量表は解釈しにくいです。因子回転によって負荷量構造を単純化すると、因子負荷量を解釈しやすくなります。ただし、回転の1つの方法があらゆる場合に最適であるとは限りません。さまざまな回転を試し、最も解釈しやすい結果が得られる回転を使用してください。回転した負荷量を並べ替えて、因子内の負荷量を明確に評価することもできます。
回転した因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 共通性 |
|---|---|---|---|---|---|
| 学歴 | 0.481 | 0.510 | 0.086 | 0.188 | 0.534 |
| 容姿 | 0.140 | 0.730 | 0.319 | 0.175 | 0.685 |
| コミュニケーション能力 | 0.203 | 0.280 | 0.802 | 0.181 | 0.795 |
| 会社への適合性 | 0.778 | 0.165 | 0.445 | 0.189 | 0.866 |
| 経歴 | 0.472 | 0.395 | -0.112 | 0.401 | 0.553 |
| 仕事への適合性 | 0.844 | 0.209 | 0.305 | 0.215 | 0.895 |
| 関心表明書 | 0.219 | 0.052 | 0.217 | 0.947 | 0.994 |
| 好感度 | 0.261 | 0.615 | 0.321 | 0.208 | 0.593 |
| 協調性 | 0.217 | 0.285 | 0.889 | 0.086 | 0.926 |
| 将来性 | 0.645 | 0.492 | 0.121 | 0.202 | 0.714 |
| 履歴書 | 0.214 | 0.365 | 0.113 | 0.789 | 0.814 |
| 自信 | 0.239 | 0.743 | 0.249 | 0.092 | 0.679 |
| 分散 | 2.5153 | 2.4880 | 2.0863 | 1.9594 | 9.0491 |
| % 分散 | 0.210 | 0.207 | 0.174 | 0.163 | 0.754 |
主要な結果:負荷量、共通性、負荷量プロット
- 会社への適合性(0.778)、仕事への適合性(0.844)、可能性(0.645)には、因子1に大きな正の負荷量があるので、この因子は、この会社における従業員適合性と成長可能性を説明します。
- 容姿(0.730)、好感度(0.615)、および自信(0.743)は、因子2に大きな正の負荷量を持つため、この因子は個人資質を説明します。
- コミュニケーション能力(0.802)と協調性(0.889)は、因子3に大きな正の負荷量を持つため、この因子は作業スキルを説明します。
- 関心表明書(0.947)と履歴書(0.789)は、因子4に大きな正の負荷量を持つため、この因子は文章力を説明します。
4つの因子全体で、データ分散の0.754(75.4%)を説明します。
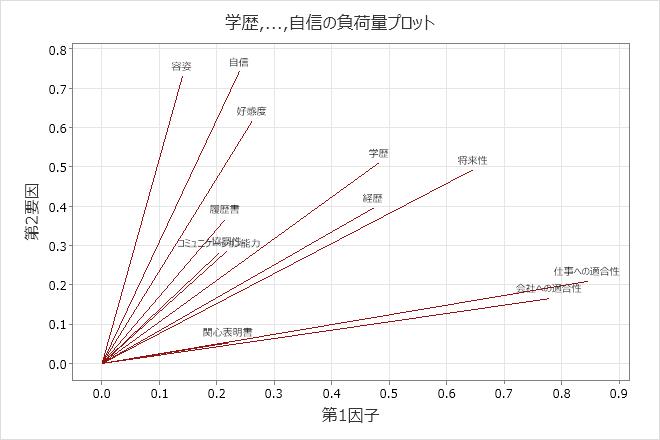
負荷量プロットは、最初の2つの因子の負荷量の結果を示します。
ステップ3:データに問題があるか確認する
最初の2つの因子が、データのほとんどの分散を説明する場合は、スコアプロットを使用してデータ構造を評価し、クラスター、外れ値、および傾向を検出できます。このプロットのデータをグループ化する場合、データ内に2つ以上の異なる分布があることを示すことがあります。データが正規分布に従い、外れ値が存在しなければ、点はゼロの値付近にランダムに分布します。

主要な結果:スコアプロット
このスコアプロットでは、データは正常で、極端な外れ値はないことがわかります。ただし、他のデータ値から離れているプロットの右下に示されるデータ値を精査したくなると思います。
ヒント
観測値ごとの計算スコアを確認するには、グラフのデータ点の上にポインタをのせます。他の因子のスコアプロットを作成するには、スコアを保存して、を使用します。
