因子負荷量
因子負荷量は、因子が変数をどの程度説明するかを示します。負荷量の範囲は-1~1です。
分析の回転方法を選択した場合、無回転因子の負荷量と回転因子の負荷量が計算されます。
解釈
負荷量パターンを調べ、各変数に対する影響が最も大きい因子を判断します。-1または1に近い負荷量は、因子が変数に強く影響していることを示します。ゼロに近い負荷量は、変数に対する因子の影響が弱いことを示します。変数によっては、複数の因子に高い負荷を与える場合もあります。
無回転の因子負荷量は解釈しにくいです。因子回転によって負荷量構造を単純化すると、より明確に、より簡単に因子負荷量を解釈できるようになることが多いです。ただし、1つの回転方法があらゆる場合に最適であるとは限りません。さまざまな回転を試し、最も解釈しやすい結果が得られる回転を使用してください。回転負荷量を並べ替えて、因子内の負荷量をより明確に評価することもできます。
- 会社への適合性(0.778)、仕事への適合性(0.844)、可能性(0.645)には、因子1に大きな正の負荷量があるので、この因子は、この会社における従業員適合性と成長可能性を説明します。
- 容姿(0.730)、好感度(0.615)、および自信(0.743)は、因子2に大きな正の負荷量を持つため、この因子は個人資質を説明します。
- コミュニケーション能力(0.802)と協調性(0.889)は、因子3に大きな正の負荷量を持つため、この因子は作業スキルを説明します。
- 関心表明書(0.947)と履歴書(0.789)は、因子4に大きな正の負荷量を持つため、この因子は文章力を説明します。
無回転の因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 共通性 |
|---|---|---|---|---|---|
| 学歴 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 容姿 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| コミュニケーション能力 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 会社への適合性 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 経歴 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 仕事への適合性 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 関心表明書 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 好感度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 協調性 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 将来性 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 履歴書 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 分散 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % 分散 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
回転した因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 共通性 |
|---|---|---|---|---|---|
| 学歴 | 0.481 | 0.510 | 0.086 | 0.188 | 0.534 |
| 容姿 | 0.140 | 0.730 | 0.319 | 0.175 | 0.685 |
| コミュニケーション能力 | 0.203 | 0.280 | 0.802 | 0.181 | 0.795 |
| 会社への適合性 | 0.778 | 0.165 | 0.445 | 0.189 | 0.866 |
| 経歴 | 0.472 | 0.395 | -0.112 | 0.401 | 0.553 |
| 仕事への適合性 | 0.844 | 0.209 | 0.305 | 0.215 | 0.895 |
| 関心表明書 | 0.219 | 0.052 | 0.217 | 0.947 | 0.994 |
| 好感度 | 0.261 | 0.615 | 0.321 | 0.208 | 0.593 |
| 協調性 | 0.217 | 0.285 | 0.889 | 0.086 | 0.926 |
| 将来性 | 0.645 | 0.492 | 0.121 | 0.202 | 0.714 |
| 履歴書 | 0.214 | 0.365 | 0.113 | 0.789 | 0.814 |
| 自信 | 0.239 | 0.743 | 0.249 | 0.092 | 0.679 |
| 分散 | 2.5153 | 2.4880 | 2.0863 | 1.9594 | 9.0491 |
| % 分散 | 0.210 | 0.207 | 0.174 | 0.163 | 0.754 |
共通性
共通性は、因子によって説明される各変数のばらつきの比率です。共通性の値は、分析の無回転因子負荷量を使用しても、回転因子負荷量を使用しても変わりません。
解釈
共通性の値を調べて、各変数が因子によってどの程度説明できるかを評価します。共通性が1に近いほど、変数は因子によって良好に説明されます。特定の変数の適合に著しく寄与する因子があれば、それを追加できます。
無回転の因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 共通性 |
|---|---|---|---|---|---|
| 学歴 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 容姿 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| コミュニケーション能力 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 会社への適合性 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 経歴 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 仕事への適合性 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 関心表明書 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 好感度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 協調性 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 将来性 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 履歴書 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 分散 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % 分散 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
これらの結果では、4因子は12の変数から抽出されます。4因子の共通性の値は、一般的にすべての変数で高く、変数は4因子で十分に表現できることを示しています。たとえば、仕事への適合性の変動率0.895(89.5%)は、4因子によって説明されます。
分散
各因子によって説明されるデータのばらつきです。主成分抽出法を使用し、負荷量を回転しない場合、各因子の分散はその固有値と等しくなります。回転は、すべての因子で説明される全体の分散を変化させずに、因子ごとに説明される分散比率の分布を変化させます。
解釈
因子ごとの分散を調べます。分散が高いほど、因子が説明するデータのばらつきが大きくなります。分析で抽出する因子数が分からない場合、まず主成分抽出法を用い、回転させずに、デフォルトの因子数(因子の最大数を抽出)を予備評価として使用できます。その後、重要な因子を、特定の値よりも大きな分散(固有値)を持つ因子として定義します。たとえば、固有値に最低でも1を持つ因子を含めることが1つの基準です。別な方法は、固有値がほとんど変化を示さず、0に近づく点を判断するために、固有値(Scree)プロットの固有値を視覚的に評価する方法です。詳細は固有値プロットのトピックを参照してください。
無回転の因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 因子5 | 因子6 | 因子7 | 因子8 | 因子9 | 因子10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 学歴 | 0.726 | 0.336 | -0.326 | 0.104 | -0.354 | -0.099 | 0.233 | 0.147 | 0.097 | -0.142 |
| 容姿 | 0.719 | -0.271 | -0.163 | -0.400 | -0.148 | -0.362 | -0.195 | -0.151 | 0.082 | 0.016 |
| コミュニケーション能力 | 0.712 | -0.446 | 0.255 | 0.229 | -0.319 | 0.119 | 0.032 | 0.088 | 0.023 | 0.204 |
| 会社への適合性 | 0.802 | -0.060 | 0.048 | 0.428 | 0.306 | -0.137 | -0.067 | 0.105 | -0.019 | -0.067 |
| 経歴 | 0.644 | 0.605 | -0.182 | -0.037 | -0.092 | 0.317 | -0.209 | -0.102 | 0.121 | 0.039 |
| 仕事への適合性 | 0.813 | 0.078 | -0.029 | 0.365 | 0.368 | -0.067 | -0.025 | -0.032 | 0.146 | 0.066 |
| 関心表明書 | 0.625 | 0.327 | 0.654 | -0.134 | 0.031 | 0.025 | 0.017 | -0.113 | -0.079 | -0.130 |
| 好感度 | 0.739 | -0.295 | -0.117 | -0.346 | 0.249 | 0.140 | 0.353 | -0.142 | 0.051 | 0.022 |
| 協調性 | 0.706 | -0.540 | 0.140 | 0.247 | -0.217 | 0.136 | -0.080 | -0.105 | -0.020 | -0.162 |
| 将来性 | 0.814 | 0.290 | -0.326 | 0.167 | -0.068 | -0.073 | 0.048 | -0.112 | -0.290 | 0.100 |
| 履歴書 | 0.709 | 0.298 | 0.465 | -0.343 | -0.022 | -0.107 | 0.024 | 0.170 | 0.008 | 0.090 |
| 自信 | 0.719 | -0.262 | -0.294 | -0.409 | 0.175 | 0.179 | -0.159 | 0.230 | -0.098 | -0.061 |
| 分散 | 6.3876 | 1.4885 | 1.1045 | 1.0516 | 0.6325 | 0.3670 | 0.3016 | 0.2129 | 0.1557 | 0.1379 |
| % 分散 | 0.532 | 0.124 | 0.092 | 0.088 | 0.053 | 0.031 | 0.025 | 0.018 | 0.013 | 0.011 |
| 変数 | 因子11 | 因子12 | 共通性 |
|---|---|---|---|
| 学歴 | -0.026 | -0.031 | 1.000 |
| 容姿 | 0.020 | -0.038 | 1.000 |
| コミュニケーション能力 | 0.012 | -0.100 | 1.000 |
| 会社への適合性 | 0.188 | -0.021 | 1.000 |
| 経歴 | 0.077 | 0.009 | 1.000 |
| 仕事への適合性 | -0.176 | 0.008 | 1.000 |
| 関心表明書 | -0.043 | -0.127 | 1.000 |
| 好感度 | 0.064 | 0.012 | 1.000 |
| 協調性 | -0.032 | 0.136 | 1.000 |
| 将来性 | -0.023 | 0.028 | 1.000 |
| 履歴書 | 0.010 | 0.156 | 1.000 |
| 自信 | -0.065 | -0.047 | 1.000 |
| 分散 | 0.0851 | 0.0750 | 12.0000 |
| % 分散 | 0.007 | 0.006 | 1.000 |
この分析は、主成分法とデフォルト設定(無回転)を使用して実行します。最初の4つの因子の分散(固有値)は1よりも大きいです。7個以上の因子を使用する場合、固有値の変化は著しく少なくなります。このため、4因子はデータのばらつきの大部分を説明します。こうした予備の結果に基づいて、因子分析を繰り返して4因子のみを抽出し、さまざまな回転を試します。
分散%
分散(分散%)の割合は、因子ごとに説明されるデータのばらつきの比率です。分散%の値の範囲は0~1(0~100%)です。
解釈
因子ごとの分散%の値を調べます。分散%の値が高いほど、因子が説明するばらつきが大きくなることを示します。したがって、分散%の値を使用して、最も重要な因子を決定できます。
分散%の共通性の値は、分析のすべての因子によって全体の分散が説明されることを示します。分析に使用する因子数がデータ内の全体の分散の十分な量を説明するかどうかを判断しやするくするために、この値を使用します。
無回転の因子負荷量と共通性
| 変数 | 因子1 | 因子2 | 因子3 | 因子4 | 共通性 |
|---|---|---|---|---|---|
| 学歴 | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| 容姿 | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| コミュニケーション能力 | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| 会社への適合性 | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| 経歴 | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| 仕事への適合性 | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| 関心表明書 | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| 好感度 | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| 協調性 | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| 将来性 | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| 履歴書 | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| 自信 | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| 分散 | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % 分散 | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
これらの結果では、データのばらつきの0.303(30.3%)は因子1によって説明されます。4つの因子全体で、0.754(75.4%)、つまりデータ内のばらつきを説明します。
因子スコア係数
因子係数は、因子分析において、成分の各変数の相対的な重みを示します。係数の絶対値が大きくなるほど、成分を計算するうえで対応する変数が重要になります。Minitabは、因子の係数を使用して因子のスコア(因子の推定値でもある)を計算します。Minitabでは、平均値を減算することでデータをスケーリングして中央に集めた後、(因子1、因子2などの下に示される)因子スコア係数とデータを乗算して因子スコアを計算します。
解釈
- 観測値の傾向を調べます。
- 回帰分析や多変量分散分析などの他の分析で使用します。
注
因子スコアの計算に推定された係数を使用するには、変数を標準化する必要があります。
固有値(Scree)プロット
screeプロットは、因子数とその対応する固有値との関係を表示します。固有値(Scree)プロットは固有値を最大値から最小値に並べます。回転を行わない場合、相関行列の固有値は因子の分散と等しくなります。
固有値プロットを表示するには、グラフをクリックして、分析を実行するときに固有値プロットを選択する必要があります。
解釈
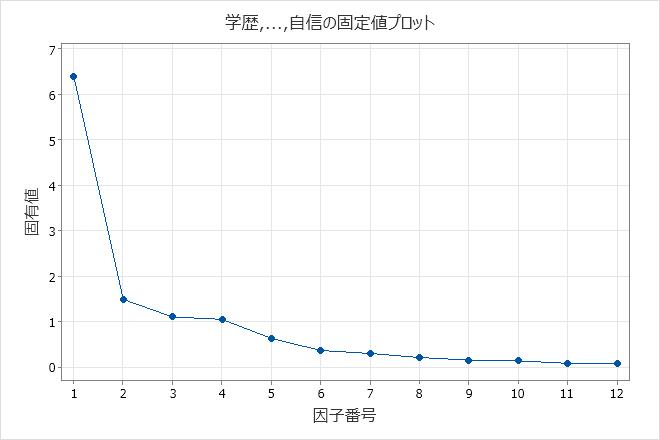
この固有値(Scree)プロットでは、最初の4つの因子が、(固有値で決まる)データの全変動の大部分を占めています。最初の4つの因子の固有値はすべて、1より大きいです。残りの因子は、分散における割合が極めて小さく、重要ではない可能性が高いです。
スコアプロット
スコアプロットは、第1因子スコアと第2因子スコアとの関係をグラフにします。
スコアプロットを表示するには、グラフをクリックして、分析を実行するときにスコアプロットを選択する必要があります。
解釈
最初の2つの成分が、データのほとんどの分散を説明する場合は、スコアプロットを使用してデータ構造を評価し、クラスター、外れ値、および傾向を検出できます。プロット上のデータをグループ化する場合、データ内に2つ以上の異なる分布があることを示します。データが正規分布に従い、外れ値が存在しなければ、点はゼロの値付近にランダムに分布します。

このスコアプロットでは、データは正常で、極端な外れ値はないことがわかります。ただし、他のデータ値から離れているプロットの右下に示されるデータ値を精査したくなると思います。
ヒント
観測値ごとに計算されたスコアを確認するには、ポインタをグラフのデータ点の上に置きます。 他の因子のスコアプロットを作成するには、スコアを保存し、を使用します。
負荷量プロット
負荷量プロットは、最初の因子の変数ごとの回転因子負荷量対二番目の因子の回転因子負荷量をグラフ化します。
負荷量プロットを表示するには、グラフをクリックして、分析を実行するときに負荷量プロットを選択する必要があります。
解釈
負荷量プロットを使用して、どの変数が因子に最大の効果があるかを特定します。負荷量は-1~1の範囲です。-1または1に近い負荷量は、変数に対する因子の影響が強いことを示します。ゼロに近い負荷量は、変数に対する因子の影響が弱いことを示します。負荷量の評価により、変数の観点から、各因子を特徴づけやすくすることもできます。因子数を選択したら、因子負荷量を解釈しやすいように別の回転を行います。
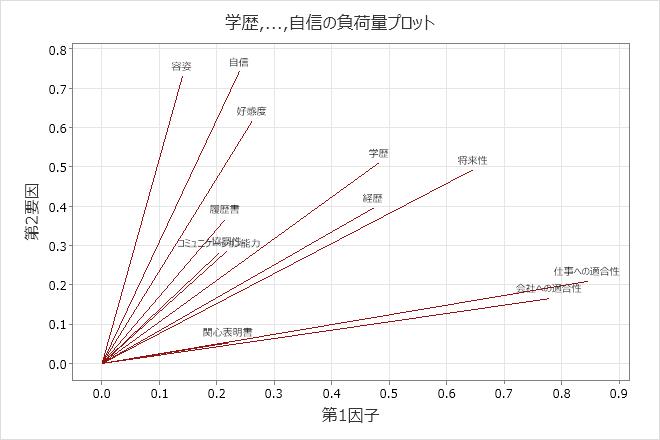
こうした負荷量プロットでは、バリマックス回転はデータ上で実行され、最初の2つの因子は解釈しやすくなります。仕事への適合性と会社への適合性には、因子1に大きな正の負荷量があるので、この因子は、申請者の地位に対する適合性を説明します。容姿、好感度、および自信は、因子2で大きな正の負荷量を持つため、この因子は申請者の「個人資質」を説明します。
バイプロット
バイプロットではスコアプロットと負荷量プロットが重ね合わて表示されます。
バイプロットを表示するには、グラフをクリックして、分析を実行するときにバイプロットを選択する必要があります。
解釈
1つのグラフにある最初の2つの因子のデータ構造と負荷量を評価するには、バイプロットを使用します。Minitabでは、第2因子スコアと第1因子スコアだけでなく、両方の因子の負荷量をプロットします。
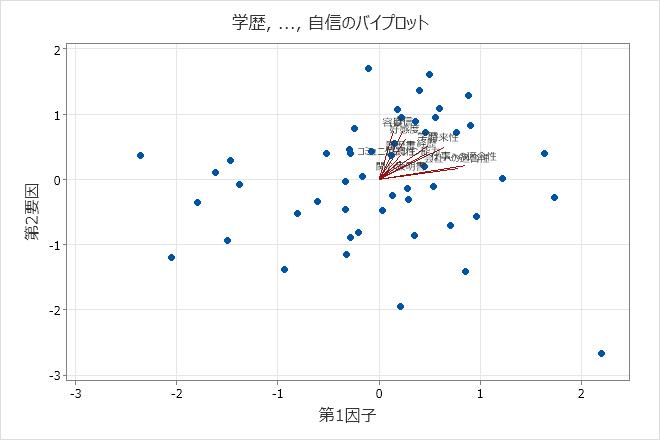
- データは正常で、極端な外れ値はないことがわかります。ただし、他のデータ値から離れているプロットの右下に示されるデータ値を精査したくなると思います。
- 会社への適合性と仕事への適合性には、因子1に大きな正の負荷量があるので、この因子は、申請者の地位に対する適正を説明します。
- 容姿、好感度、および自信は、因子2に大きな正の負荷量があるので、この因子は、申請者の個人資質を説明します。
