二乗距離
二乗マハラノビス距離~一般形
線形判別におけるグループtの観測値xとグループの中心(平均)との二乗距離(マハラノビス距離とも呼ばれる)は、次の一般形で求められます。

二乗マハラノビス距離~2次関数
2次判別関数におけるxからグループtまでの二乗マハラノビス距離は次のように計算します。

一般化平方距離~線形関数
線形判別関数におけるxからグループtの一般化された二乗距離は次のように計算されます。
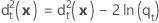
一般化平方距離~2次関数
2次判別関数におけるxからグループtの一般化された二乗距離は次のように計算されます。

事後確率
グループtに属するxの事後確率は次のように計算されます。
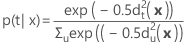
線形判別スコア
線形判別スコアは次のように計算されます。

表記
| 用語 | 説明 |
|---|---|
| x | この観測値の予測変数の値を含む長さpの列ベクトル(この列ベクトルは1つの行として保存されます) |
| p | 予測変数の数 |
| n | 合計観測数 |
| t | グループのサブスクリプト |
| nt | グループtに含まれる観測値の数 |
| qt | グループtの事前確率(nt/nに等しい) |
| Sp | 線形判別分析の併合共分散行列 |
| Si | 2次判別分析のグループiの共分散行列 |
| mt | グループtのデータから計算される予測変数の平均を含む長さpの列ベクトル |
| St | グループtの共分散行列 |
| |St| | Stの行列式 |
線形判別関数
線形判別関数は、重回帰分析の回帰係数に相当し、次のように計算します。


xが任意の場合、このルールでは、xを線形判別関数が最大のグループに割り当てます。
表記
| 用語 | 説明 |
|---|---|
| x | この観測値の予測変数の値を含む長さpの列ベクトル(この列ベクトルは1つの行として保存されます) |
| mi | グループiのデータから計算される予測変数の平均を含む長さpの列ベクトル |
| Sp | 併合共分散行列 |
| ln pi | グループiの事前確率の自然対数 |
一般化平方距離
一般化平方距離は、2次距離の測度として使用され、次のように計算します。


表記
| 用語 | 説明 |
|---|---|
| x | この観測値の予測変数の値を含む長さpの列ベクトル(この列ベクトルは1つの行に保存されます) |
| mi | グループiのデータから計算される予測変数の平均を含む長さpの列ベクトル |
| Sp | 併合共分散行列f |
| ln pi | グループiの事前確率の自然対数 |
事後確率
事後確率は、データが与えられたグループiの確率で、次のように計算されます。
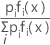
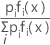
最大事後確率は、ln [pi fi (x)]の最大値と等しくなります。
(分布が正規分布の場合):


および


表記
| 用語 | 説明 |
|---|---|
| pi | グループiの事前確率 |
| fi(x) | グループiのデータの同時密度(母集団パラメータをサンプル推定値に置き換え) |
