平均
平均リンケージ法では、2つのクラスター間の距離は、一方のクラスター内の変数と他方のクラスター内の変数間の平均距離です。平均距離は、次の距離行列で計算されます。

表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIから成るマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
| Nk | 変数クラスターkの数 |
| Nl | クラスターlの変数の数 |
| Nm | クラスターmの変数の数 |
重心
重心リンケージ法では、2つのクラスター間の距離は、クラスター重心間の距離つまり平均値です。距離は、次の距離行列で計算されます。
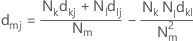
表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIから成るマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
| Nk | 変数クラスターkの数 |
| Nl | クラスターlの変数の数 |
| Nm | クラスターmの変数の数 |
完全連結法
完全連結法(最遠隣法とも呼ばれる)では、2つのクラスター間の距離は、一方のクラスター内の変数と他方のクラスター内の変数間の最大距離です。最大距離は、次の距離行列で計算されます。
dmj = max (dkj, dlj)
表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIからなるマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
類似度分析(McQuitty)
類似度連結法を使用する場合、距離は次の距離行列を用いて計算します。

表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIからなるマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
中央値
中央値リンケージ法では、2つのクラスター間の距離は、一方のクラスター内の変数と他方のクラスター内の変数間の中央値距離です。中央値距離は、次の距離行列で計算されます。

表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIから成るマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
| dkl | クラスターkとlの距離 |
単連結
単連結法(最近隣法)では、2つのクラスター間の距離は、一方のクラスター内の変数と他方のクラスター内の変数間の最小距離です。
距離は、次の距離行列で計算されます。
dmj = min (dkj, dlj)
表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIから成るマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
ウォード(Ward)
ウォード(Ward)リンケージ法では、2つのクラスター間の距離は、点から重心までの平方偏差の和です。ウォード・リンケージ法の目的は、クラスター内平方和を最小にすることです。距離は、次の距離行列で計算されます。

注
ウォード(Ward)リンケージ法では、2つのクラスター間の距離が、元の距離行列Dの最大値d(max)より大きくなる可能性があります。この場合、類似度は負になります。
表記
| 用語 | 説明 |
|---|---|
| dmj | クラスターmとjの距離 |
| m | クラスターkとIからなるマージされたクラスター(m = (k,i)) |
| dkj | クラスターkとjの距離 |
| dlj | クラスターlとjの距離 |
| dkl | クラスターkとlの距離 |
| Nj | クラスターjの変数の数 |
| Nk | クラスターkの変数の数 |
| Nl | クラスターlの変数の数 |
| Nm | クラスターmの変数の数 |
