三角座標系では、3つの成分がある混合における成分間の関係を視覚化できます。混合の成分は、加算したときに一定の合計量となる必要があるため、互いに制約し合っていると言うことができます。ここで使用する三角座標系では、x1、x2、x3成分の最小値が0、最大値が1になっています。
次の図は、三角座標系の一般的なレイアウトです。混合モデルの各成分は、合計量を1とした場合に、その合計量に対する比率として説明されます。三角形の各頂点は、純粋混合(1成分ブレンドとも呼ばれる)を表しています。純粋混合では、1つの成分の比率が1で、その他の成分は0です。

三角形の辺上にある点は、成分のうち1つが欠けている配合を表します。次の図は、いろいろな種類の配合の位置を示しています。

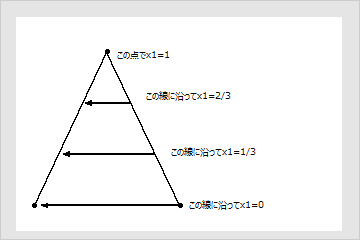

次は、座標系上の点をいくつか見てみましょう。
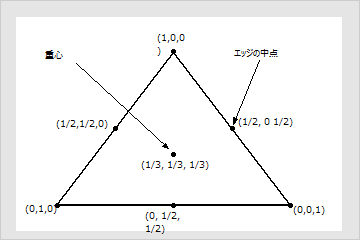
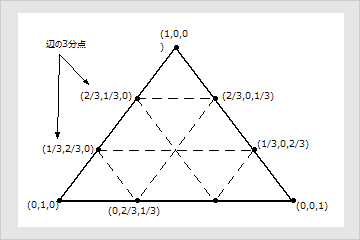
前の図で紹介されている三角上の各点は、それぞれ異なる配合を表しています。次に例を示します。
- 辺の中間点は、2つの成分から成る混合で、1つが混合の1/2を、もう1つが1/2を占めています。
- 辺の3分点は、2つの成分から成る混合で、1つが混合の1/3を、もう1つが2/3を占めています。これらの点は三角形の辺を3等分しています。
- 中心点(または重心)は、すべての成分が等しい比率(1/3、1/3、1/3)を占めている完全混合を表します。完全混合とは、計画空間の内部に位置し、欠けている成分がないものを指します。
